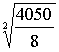Consigne

TESTS D’ALGEBRE N° 16

Corrigé

Exercices et problèmes d' applications en lien avec les racines carrées.

Série: d'Exercices

On dit que :

Dans un triangle rectangle le "carré" du grand coté (hypoténuse) est égal à la somme des "carrés" des longueurs des cotés formant l’angle droit .

Pythagore

On vous demande de calculer l’hypoténuse d’un triangle rectangle dont les cotés de l’angle droit valent respectivement :

SOS Cours

Racines carrées

1 °) 8 cm et 6 cm	a =	a =	a =10 cm
2°) 12 m et 9 m	a =	a =	15 m
3°) 165 mm et 92 mm	a =	a =	188,91532 mm
4°) 125 m et32,7dam	a =	a =	350,07713 m

Problème :1

L’hypoténuse d’un triangle rectangle se calcule en utilisant la formule suivante:

a = ; dans laquelle b et c sont les mesures des deux cotés formant l’angle droit.

Calculer la longueur de l’hypoténuse d’un triangle rectangle dont les longueurs des cotés de l’angle droit sont : c = 0,35 dm et b = 0,84 dm

a = donc : a^2 = b^2 + c^2

donc : a^2 = 0,84^2 + 0,35^2 calcul: 0,84^2=0,7056 0,35^2=0,1225 a^2 =0,8281 a = a=0,91 dm

Problème :2

L’hypoténuse d’un triangle rectangle se calcule en utilisant la formule suivante:

a = ; dans laquelle b et c sont les mesures des deux cotés formant l’angle droit.

Calculer la longueur du coté "c" , sachant que a = 50 cm et b = 30cm

a = donc : a^2 = b^2 + c^2

50^2 = 30^2 + c^2 2500 = 900 + c^2 2500 -900 = c^2 1600 = c^2 = c = 40 cm

Problème :3

L’hypoténuse d’un triangle rectangle se calcule en utilisant la formule suivante:

a = ; dans laquelle b et c sont les mesures des deux cotés formant l’angle droit.

Calculer la longueur du coté "b" , sachant que c= 24 dm et a= 400 mm

a = 40 dm a = donc : a^2 = b^2 + c^2

40^2 = b^2 + 24^2 40^2- 24^2 = b^2 1600- 576 = b^2 1024 = b^2 = 32 = b

Problème :4

L’ aire d’un carré est de 2735,29 dm²

question : donner la valeur de la mesure d’un coté en dm puis mm

C =

52,3dm

5230mm

Problème :5

Calculer le rayon d’un cercle dont l’aire est de 2826 cm²

On prendra 3,14 pour « py »

Aire du disque = 3,14R^2	2826 cm^2= 3,14 R^2	R^2 = 2826:3,14
		R^2 =900 cm^2
R =	R = 30 cm

Problème :6

Calculer la valeur du diamètre d’un cercle dont l’aire est de 14949,54 cm²

On prendra 3,14 pour « py »

Solution 1 : on prend l'Aire du disque = 3,14R²

D = 2R
Aire du disque = 3,14R^2	14949,54= 3,14 R^2	R^2 = 14949,54:3,14
		R^2 =4761cm^2
R =	R = 69 cm	Donc D = 138 cm

Solution 2: on prend l'Aire du disque = 3,14(D²/4 )

On trouve D = 138 cm

Problème :7

La puissance électrique consommée dans une résistance est donnée par la formule

P = R x I² dans laquelle R est la mesure de la résistance et I celle de l’ intensité.

Transformer la formule pour que nous puissions calculer I ( I = ? )

Calculer l’intensité « I » si P = 4050 Watts et R = 8 ohms

P = R x I^2	4050 = 8 x I^2
I =		I = 22,5 ampères
I = 22,5 A

Problème :8

Type d’exercice : Rechercher la longueur du coté d’un carré ( petit "cé" « c ») dont on connaît son aire (« cé » au carré s’écrit en langage mathématique:    c ² ).

L’aire d'un carré est de 81 m² ; donner la longueur du coté

Comme c ^2=81m^2.
pour trouver « c »; j’écrirai que =
c =	c =
	c= 9 m^1 c = soit plus simplement : 9 m
conclusion :le carré de 81 m^2 à pour coté 9