|
= Savoir connaître et savoir utiliser les 3 relations de
trigonométrie : sin ; cos ; tan . |
|
TESTS : Corrigé
|
LECON : |
|
N°22-1 |
|
CONTROLE : |
1°) Donnez
la définition littérale du « sinus »
2°) Donnez la définition littérale du
« cosinus »
3°) Donnez la définition littérale de la
« tangente »
4°) Traduire sous forme d’une égalité mathématique
la définition du « sinus ».
(A partir de cette
égalité donnez les transformations possibles.)
5°) Traduire sous forme d’une égalité mathématique
la définition du « cosinus ».
(A partir de cette
égalité donnez les transformations possibles.)
6°) Traduire sous forme d’une égalité mathématique
la définition de la « tangente ».
(A partir de cette égalité
donnez les transformations possibles.)
7° ) Construire un
triangle rectangle , nommez les cotés et les angles , et transformez les égalités ci dessus .
|
EVALUATION : |
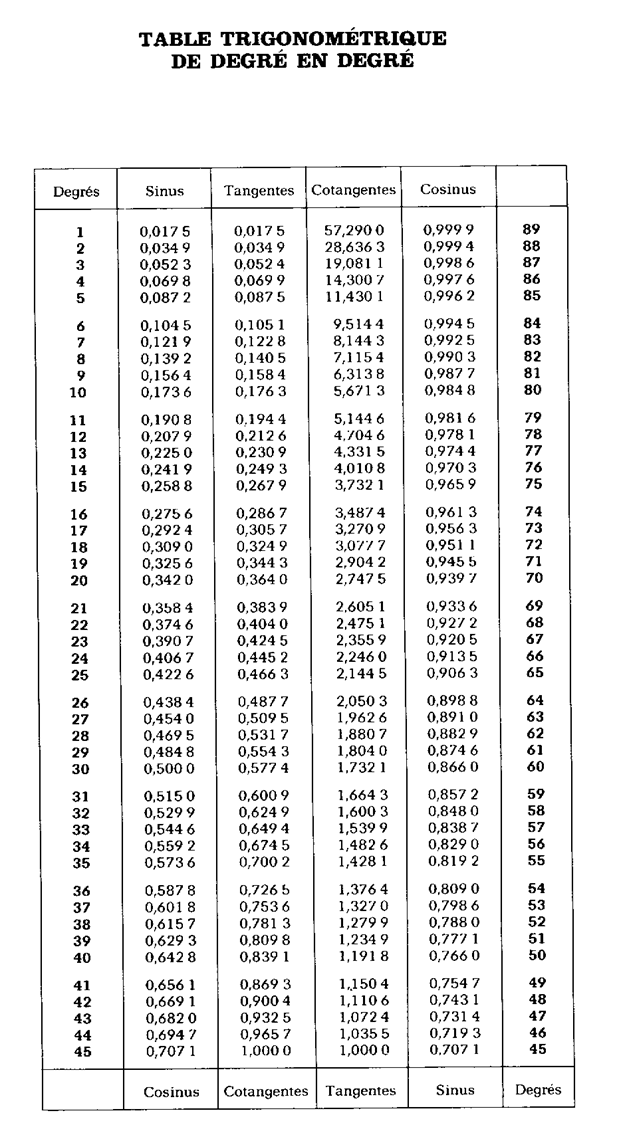
Partie 1: Utilisation de la table jointe
et de la calculatrice.
Les
valeurs à reporter sont celles lues sur la table et celles sur l’écran de la calculatrice. A vous
de tirer une conclusion !!!
Compléter les tableaux :
pour b = 22°
|
|
avec la table |
avec la calculatrice |
|
sinus b |
|
|
|
cosinus b |
|
|
|
tangente b |
|
|
|
cotangente b |
|
|
pour a = 68 °
|
|
avec la table |
avec la calculatrice |
|
sinus a |
|
|
|
cosinus a |
|
|
|
tangente a |
|
|
|
cotangente a |
|
|
Quels commentaires vous suscitent la comparaison
des deux tableaux ?
Recherchez la valeur de l’angle en degré:
|
|
avec la table |
avec la calculatrice |
|
sinus a = 0,866 |
|
|
|
cosinus a = 0,866 |
|
|
|
tangente a = 1,732 |
|
|
|
cotangente a = 1,732 |
|
|
il faudrait donner la valeur de l’angle en valeur dans
le système décimale , et en système sexagésimal
. !
Partie
2
I )
Le triangle ABC est rectangle en B :
Compléter le tableau (les résultats seront exprimés en mm )
C c B

|
a |
12 dm |
|
|
|
|
b |
|
|
|
|
|
c |
|
|
1,25 dam |
|
En
plus : Commentez les
résultats obtenus avec « a »
et « b » ; Que peut - on dire du triangle ?
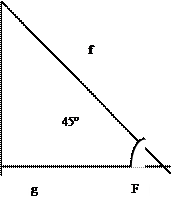
II ) Le triangle
DEF est rectangle en D
E e D
|
e |
|
|
|
|
|
f |
|
|
|
|
|
g |
|
|
2,35
dm |
|
En
plus : Commentez les
résultats : Que peut - on dire de
la figure ?
III) Le
triangle EFG est un triangle
quelconque ; « h » est la
hauteur (
h b

|
|