|
DOSSIER : THALES : interdisciplinarités |
||
|
1°) Enoncer le théorème de
Thalès .( vous aider d'un croquis) (sos
cours) |
||
|
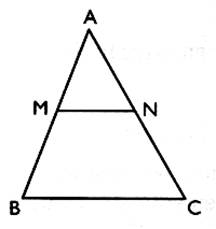
Série 1 : 1°) Dans un triangle ACB ,
le segment MN est parallèle au
segment BC . |
||
|
a)
On
donne AN = 8 , AC = 12 et AB = 15 .
Calculer AM. AM = 10 b)
On donne AM = 4 , AB = 5 et AN = 5 . Calculer AC.= 6,25 |
|
|
|
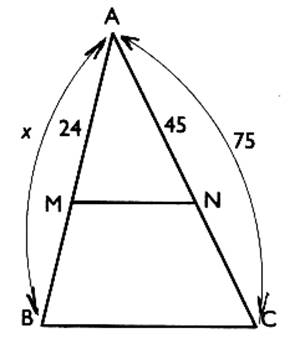
2°) Dans le triangle ACB ,
la droite ( MN ) est parallèle à la droite ( B C ) . Calculer la longueur " x " .
= 40 |
|
|
|
|
||
|
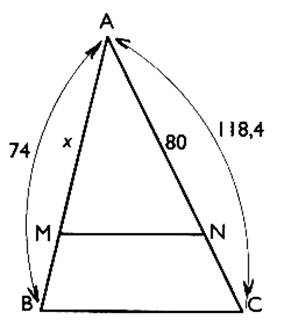
3°) Dans le triangle ACB ,
la droite ( MN ) est parallèle à la droite ( B C ) .Calculer la longueur " x " . X= 50 |
|
|
|
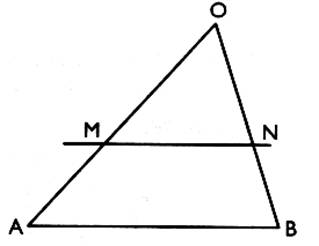
4°) Sachant que ( AB) est parallèle à ( M N ) .On demande de calculer OM lorsque ON = 14 ; OA = 27 et OB = 21 . En déduire que MA et
NB . OM = 18 |
|
|
|
Vérifier que les
rapports MA / NB = OM / ON = OA / OB
. recherche du même coefficient |
||
|
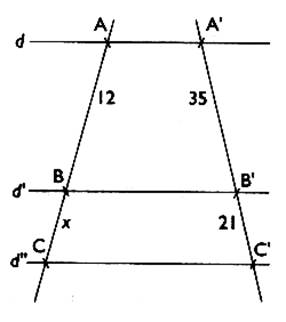
5°) Calculer la longueur "x" , sachant
que les droites d , d' et d"
sont parallèles ; Les dimensions sont en mm . X =
7,2 |
|
|
|
Série
2 : PROBLEMES : 1°) Droite des milieux
d' un triangle . a) Construire un triangle de côtés
AB = b)Appliquer la relation de Thalès pour prouver que N est le milieu de [ AC] . La droite ( MN ) est dite « droite des milieux » . b) Construire les deux autres droites des milieux du triangle . |
||
|
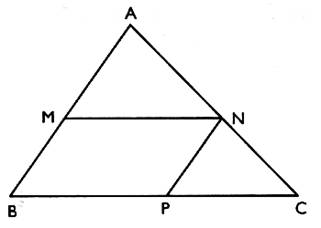
2°) Dans un triangle ACB , on trace le segment MN parallèle au segment BC et le segment NP parallèle au
segment AB . On donne AB = 5 ; BC = 7 ; AC = 6 et AM = 3 |
|
|
|
répondre aux question suivantes : a) calculer AN en appliquant la relation de Thalès au triangle ABC
coupé par MN . En déduire CN . b) Calculer CP en appliquant la relation de Thalès au triangle CBA coupé par le segment
NP. En déduire BP . c) Quelle est la nature du quadrilatère MNPB ? En déduire MN . d) Calculer le rapport MN / BC . Vérifier que l’on a : |
||
|
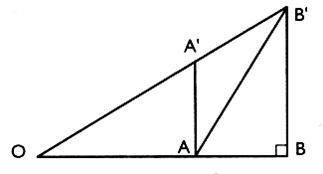
3°) La figure ci - dessous représente un élément
de charpente pour lequel on
a : OA = a) calculer
dans le triangle rectangle ABB’ : la longueur de AB pour que AB’=AO. b) Calculer la longueur OB puis OB’ dans le
triangle B’BO . c) Sachant que A’A est parallèle à
B’B , calculer A’A en utilisant le résultat de la question
précédente . d) Calculer A’O en utilisant la propriété de Thalès . |
|
|
|
Série
3 : en utilisant « Thalès et Pythagore » . |
||
|
On doit calculer les différentes longueurs des
pièces des éléments de charpente ci - dessous . Pour cela , il faut appliquer
soit la propriété de Thalès et / ou la
propriété de Pythagore . Les longueurs sont indiquées en mètres . On
arrondira les résultats au cm près . ( on dit aussi : à deux décimales ) |
||
|
1°) soit la figure ci - dessous :
|
a) Calculer l’angle C . b) Quelle est la position de D sur le segment AC et de E sur le segment AB ? c) Calculer les longueurs des
segments : BC , AC , BD et DE . |
|
|
2°) soit la figure ci - dessous :
|
a) Calculer la longueur du segment AC . b) On connaît la position des points F et D sur le segment AB , en
déduire celle des points G et E sur
le segment AC . c) Quelle est la nature du triangle
GDA ? d) Calculer les longueurs des segments : AG , GE , EC , GD , GF , ED
et EB. |
|