|
Pour
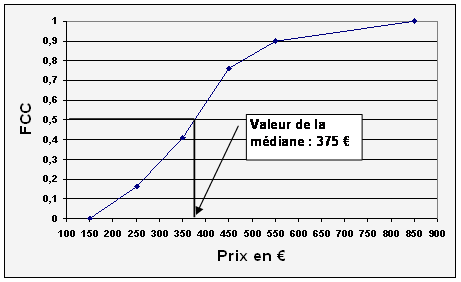
le calcul, il faut regarder dans quel intervalle se trouve la fréquence ayant
pour valeur 0,5.(50%)
Cet
intervalle est [350 ; 450 [. Or 41 % des valeurs sont comprises les
intervalles précédents. Il reste donc pour cet intervalle 9%.
Dan
l'intervalle [350 ; 450[, il y 35 % des valeurs. Il faut donc connaître la
"place" de ces 9% en considérant que les valeurs se répartissent de
manière uniforme.
35 % correspondent à 100
€
donc 1 % correspond à
100/35 = 2,85714…..€
Alors 9 % correspondent
alors à 9 ´
2,85714…=25,7142…. €
La
valeur de la médiane est donc 350 + 25,7142 = 375, 7142 €
5°)
Cet intervalle est : [ 387-138 ; 387 + 138 ]= [249 ;
525]
Comment
déterminer quel est le nombre de valeurs contenus
dans cet intervalle ?
Cet
intervalle empiète sur plusieurs classes à savoir : [150 ; 250 [ ; [250 ; 350
[ ; [350 ; 450 [ ; [ 450 ; 550 [.
En
fait on va considérer que l'effectif de chaque classes
se répartit de manière uniforme.
Dans
l'intervalle [150 ; 250 [ il y a 320 valeurs; 320
valeurs vont se répartir sur 100 €; les valeurs seront donc espacées de 100
/ 320 = 0,3125 €
Il
faut donc calculer combien de valeurs seront dans l'intervalle [249 ; 250 [.
Il
y a 1 € d'écart donc il y aura 1 / 0,3125 = 3,2 valeurs soit 3 valeurs.
Pour
les intervalles suivant :
[250 ; 350[ et [350 ;
450 [ il y a 1 200 valeurs au total.
Pour
l'intervalle [450 ; 550[ il faut calculer combien de
valeurs il y aura jusqu' à 525.
Dans l'intervalle [450 ; 550[, il y a 280
valeurs. Chaque valeur sera donc séparée de 280 / 100 = 0,28 €.
De
450 à 525 il y aura donc 75/0,28 = 267,857….soit 268 valeurs.
Au
total on aura donc dans l'intervalle [ 249 ; 525 ] :
3 + 1200 + 268 = 1471 valeurs soit un pourcentage de (1471/2000) ´ 100 = 73,55 %
|
![]()
![]()