NIVEAU IV : CORRECTION DES EXERCICES DE STATISTIQUES
Exercice n°1
a)
il
y a 8 carreaux au total don 8 ´ 5 = 40 bus ont roulé entre 140 000 km et
220 000 km
b)
Ce
sont des données regroupées en classe, on les regroupe dans un tableau :
|
Classe représentant le
nombre de kms |
Nombre de Bus |
Centre de la classe |
|
[20 000 ; 60 000[ [60 000 ; 100 000 [ [100 000 ; 140 000 [ [140 000 ; 220 000] |
30 60 40 40 |
40 000 80 000 120 000 180 000 |
|
Total |
170 |
|
On
veut calculer le kilométrage moyen ( noté ![]() . Comme les données sont regroupées en classes, les x1,
x2….xp sont les valeurs du
centre de chaque classe :
. Comme les données sont regroupées en classes, les x1,
x2….xp sont les valeurs du
centre de chaque classe :
![]() kms.
kms.
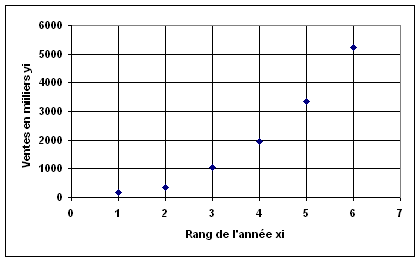
Exercice n°2
1°)
Calcul du mode
Le
mode est dans ce cas une classe modale car les données sont à variable continue
( la distance peut avoir n’importe quelle valeur).
La
classe modale correspond à l'effectif maximal donc : [ 6
000 ; 8 000 [.
Calcul
de la moyenne
Etant
donné que les données sont regroupes en classe, il faut calculer chaque centre
de classe afin d'avoir la distance moyenne parcourue par les voitures. Le
calcul est le même qu'à l'exercice n°1 :
![]() kms.
kms.
Calcul
de la médiane
La
médiane est la valeur de la variable ( la distance
ici) qui sépare l'effectif total en deux.
L'effectif
est 62, la médiane sera donc la valeur de la variable correspondant au véhicule
n°31.
Le
31eme véhicule est dans la classe [ 6000 ;
8000 [ et c'est le 11eme de cette classe. Si on considère que les 11
véhicules de cette classe se répartissent de manière égale, à ce véhicule
correspondra
8
000 km.
La
valeur de la médiane est donc de 8000 km
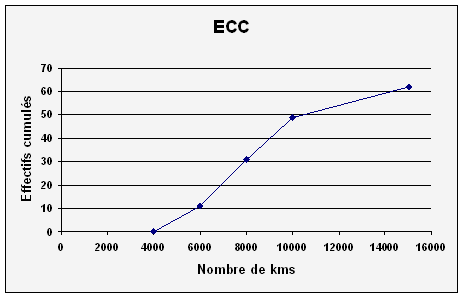
2°)
Le polygone des effectifs cumulés croissant confirme la valeur de 8000 pour la
médiane car au point d'ordonnée 31 correspond 8000 en abscisse.
Exercice n°3
1°)
La moyenne est :
![]()
Pour
calculer l'écart type, vous pouvez utiliser les fonctions statistiques de votre
calculatrice ou dans le cas contraire et, afin d'éviter les erreurs on procède
par étape pour calculer σ. Avant de calculer σ, il faut calculer V,
la variance puisque σ = √V.
Or : 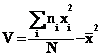
Etant
donné que les valeurs sont regroupées en classe, il faut prendre la valeur du
centre de chaque classe pour les x i, les ni étant
l'effectif de chaque classe.
|
Longueur (en cm) |
Effectif ni |
Valeur centrale xi |
Valeur nixi2 |
|
[150,4 ; 150,5[ [150,5 ; 150,6[ [150,6 ; 150,7[ [150,7 ; 150,8[ [150,8 ; 150,9 [ |
7 18 41 28 6 |
150,45 150,55 150,65 150,75 150,85 |
158446,4175 407975,445 930512,3225 636315,75 136534,335 |
|
Total |
100 |
|
2269784,27 |
On
donc : ![]()
Ainsi
![]()
2°)
L'intervalle est : [ 150,658 - 0,09867 ; 150,658 +
0,09867 ] = [ 150,55933 ; 150,75667] soit en arrondissant au dixième : [ 150,6
; 150,8] .
Cet
intervalle englobe les deux intervalles [150,6 ; 150,7[ et
[150,7 ; 150,8[ soit 41 +28 = 69 valeurs.
Etant
donné qu'il y a 100 valeurs, 69 % des pièces ont une longueur appartenant à
l'intervalle [150,8 ; 150,8].
Exercice n°4
Les
calculs ne seront pas détaillés car ils sont similaires à l'exercice n°3
1°)
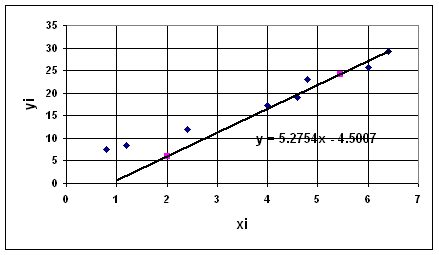
![]()
2°)
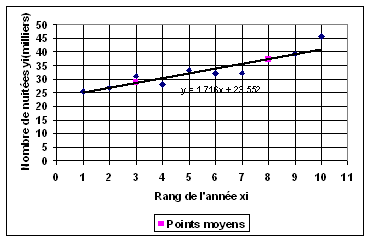
![]()
3°)
Rappel : la fréquence est le rapport de l'effectif par l'effectif total. On
l'exprime en % en multipliant ce rapport par 100. Dans cet exercice ce n'est
pas demandé.
La
somme des fréquence doit faire 1 ou 100 si elles sont
exprimées en %
|
Prix (en €) |
Effectif |
Fréquences |
FCC |
FCD |
|
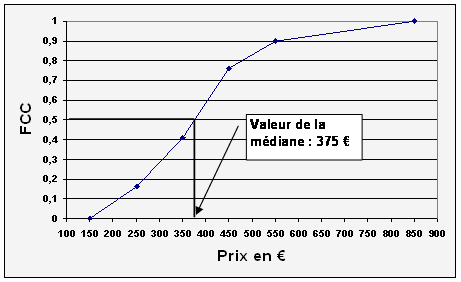
[ 150 ; 250 [ [ 250 ; 350 [ [ 350 ; 450 [ [ 450 ; 550 [ [ 550 ; 850 [ |
320 500 700 280 200 |
0,16 0,25 0,35 0,14 0,10 |
0,16 0,41 0,76 0,90 1 |
1 0;84 0,59 0,24 0,10 |
|
Total |
2 000 |
1 |
|
|