|
WARMATHS |
Equations |
- Définitions.
- Méthode de résolution:
- Ce qu'il est nécessaire de connaître.
- Règles de calculs.
- Les 6 étapes de la résolution.
- Exemples résolus:
- L'équation ne contient pas de fractions ( quotient).
- L'équation contient une ou plusieurs fractions (quotients).
- L'équation contient des x2.
- Cas particuliers.
- Résolution de problèmes:
- Mise en équation.
- Exemples simples.
- Exemples moins faciles.
|
On ne présente ici que les équations se ramenant au type ax + b =c appelées équations du premier degré à une inconnue ( en x) . |
Une équation est une égalité qui traduit une situation dans laquelle une valeur (masse, durée, somme d'argent, distance,...) est inconnue. Cette valeur est appelée l'inconnue de la situation (ou du problème). Cette inconnue est notée à l'aide d'une lettre choisie dans l'alphabet: C'est très souvent la lettre x qui est choisie mais rien ne vous oblige à vous conformer à ce choix, toute lettre pouvant faire l'affaire. L'essentiel est d'avoir un nom pour la valeur inconnue que nous devons calculer.
Calculer cette valeur inconnue c'est résoudre l'équation. Les valeurs calculées sont appelées solutions de l'équation.
Le type d'équation que nous étudierons est de la forme ax+b=c où a, b et c sont des nombres ( sous forme de
nombres décimaux ou de quotients) appelés coefficients.
Par exemple: 2x -5 = 3 où a = 2, b = -5 et c = 3.
L'expression située à gauche du signe = est appelée premier membre, celle qui est située à droite est appelée second membre de l'équation.
Méthode de résolution des équations:
En quatrième nous obtiendrons le plus souvent une seule valeur comme solution. Mais il peut arriver que nous arrivions à une impossibilité: dans ce cas il n'y a aucune valeur solution de l'équation. Il peut arriver aussi que n'importe quelle valeur convienne: dans ce cas nous dirons qu'il y a une infinité de valeurs comme solution de l'équation.
1. Ce qu'il est nécessaire de connaître:
Pour bien comprendre la suite il faut que vous sachiez utiliser les nombres relatifs (addition et multiplication) ainsi que les quotients ( réduction au même dénominateur, addition, multiplication, quotients égaux,...).
Il va , notamment, être très souvent question de nombres opposés et de nombres inverses. Aussi je vous fais un petit rappel:
**Deux nombres sont opposés lorsque leur somme est égale à 0. Par exemple:
![]()
Conséquence importante: deux nombres opposés ont la même valeur absolue et des signes différents.
Comment trouver l'opposé d'un nombre: il suffit de changer le signe de ce nombre.
**Deux nombres sont inverses l'un de l'autre lorsque leur produit est égal à 1. Par exemple:
![]()
Conséquence: un nombre et son inverse ont le même signe.
Comment trouver l'inverse d'un nombre: si le nombre est un quotient, vous inversez le quotient (le numérateur et le dénominateur échangent leur place: l'inverse de 2/3 est 3/2, l'inverse de 1/5 est 5/1 ou 5). Sinon vous écrivez 1 sur ce nombre ( l'inverse de 3 est 1/3, l'inverse de -4 est -1/4 ou 1/(-4)).
Attention:
Le nombre 0 n'a pas d'inverse
**A noter:
- Nous utiliserons l'opposé d'un nombre essentiellement dans une somme.
- Nous utiliserons l'inverse d'un nombre essentiellement dans un produit.
|
R1: Règle 1 |
R2: Règle 2 |
|
Si nous ajoutons le même nombre aux deux membres d'une égalité Alors la nouvelle égalité a les mêmes solutions. Exemple: x+1=2 et x+1+(-1)=2+(-1) conduisent à la même valeur solution: x=1 |
Si nous multiplions par le même nombre les deux membres d'une égalité Alors la nouvelle égalité a les mêmes solutions. Exemple: 2x=6 et 2x.(1/2)=6.(1/2) conduisent à la même valeur solution: x=3 |
Remarques: dans la résolution des équations
- pour la règle R1 nous ajoutons, dans les deux membres, l'opposé du nombre que nous désirons faire "disparaître". Ce nombre doit être un élément (opérande) d'une somme (comme le 1 dans x+1).
- pour la règle R2 nous multiplions les deux membres, par l'inverse du nombre à "éliminer". Ce nombre doit être l'un des facteurs d'un produit (comme le 2 dans 2x)
3. Les 6 étapes de la résolution:
Le but est de trouver les valeurs de x. Il faut manipuler l'équation proposée (en utilisant les règles R1 et R2) de façon à ce qu'elle se transforme en une équation de la forme: x=... (lorsque c'est possible). Pour mieux comprendre la méthode, nous allons suivre pas à pas la résolution de l'équation:
2(x-1)-3=-3-4+5x
Etape 1:
« Réduire » les expressions dans les deux membres, c'est à dire effectuer tous les calculs possibles.
Exemple: 2(x-1)-3=-3-4+5x devient 2x-2-3=-7+3x puis 2x-5=-7+5x
Etape 2:
Puis s'arranger pour que les termes en « x » se retrouvent dans le même membre (Réunir).
Exemple: reprenons l'égalité calculée ci-dessus (en vert). Nous devons faire en sorte que les expressions contenant l'inconnue x (2x dans le 1er membre et 3x dans le second) soient réunies dans l'un des membres et les nombres comme -5 et -7 soient réunis dans l'autre membre. Pour les x il suffit d'enlever 2x dans les deux membres en ajoutant son opposé (-2x) dans les deux membres:
2x-5-2x=-7+5x-2x
Etape 3:
Simplifier chaque membre (Simplifier dans les deux membres).
Nous avons: 0-5=-7+x dans le 1er membre 2x-2x=0 et dans le second 5x-2x=3x
D'où: -5=-7+3x
pour les nombres il suffit d'ajouter l'opposé de -7 (c'est à dire +7) aux deux membres:
-5+7=-7+3x+7 et simplifier: 2=3x
Etape 4:
Et enfin, trouver la solution (Calculer la valeur de x).
Nous avons 3x dans le second membre ce qui représente le produit de 3 par x
Pour obtenir 1x ou x il suffit de multiplier 3x par l'inverse de 3 (c'est à dire 1/3) sans oublier de multiplier le contenu de l'autre membre (c'est à dire 2) par cet inverse: 2.1/3=3x.1/3 soit 2/3=x
Etape 5 et 6:
Il ne reste plus qu'à vérifier la valeur trouvée (Vérifier) et à conclure (Conclure).
Au départ l'équation était:
2(x-1)-3=-3-4+5x.
Si nous remplaçons x par la valeur trouvée (2/3), la valeur prise par le premier membre doit être égale à celle du second membre:
|
1er membre: 2(2/3-1)-3 2(2/3-3/3)-3 2(-1/3)-3 -2/3-9/3 -11/3 |
2ème membre: -3-4+5x -7+5(2/3) -7+10/3 -21/3+10/3 -11/3 |
Nous trouvons donc une solution: x=2/3 (Attention: ne pas confondre avec -11/3 qui est la valeur de chaque membre lorsque x=2/3...!)
Nous avons bien six étapes, pas une de plus. Et bien souvent vous pourrez passer une ou plusieurs étapes mais toujours dans le même ordre:
|
Etape 1 |
Réduire |
|
Etape 2 |
Réunir |
|
Etape 3 |
Simplifier |
|
Etape 4 |
Calculer |
|
Etape 5 |
Vérifier |
|
Etape 6 |
Conclure |
Remarques:
Réunir et Simplifier se font pratiquement ensemble.
Pour vérifier la validité d'une valeur solution (c'est à dire prouver que la valeur calculée est bien solution de l'équation) il n'y a qu'une seule façon de s'y prendre: remplacer l'inconnue par cette valeur dans chaque membre séparément. Exemple: vérifier que 4 est solution de 2(x+3)=5-3(1-x). Nous devons écrire:
1er membre: 2(4+3)=2.7=14
2ème membre: 5-3(1-4)=5-3.(-3)=5+9=14
chaque membre étant égal à 14, l'égalité est bien vérifiée. La valeur 4 est solution de l'équation (c'est d'ailleurs la seule).
Pour illustrer tout ceci voyez les exemples ci-dessous.
Exemples de résolutions d'équations:
1. L'équation ne contient pas de quotients:
Exemple 1:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etapes |
|
4 x + 1 = 9 |
|
Réduire |
|
4x+1-1=9-1 (R1) 4x=8 |
Réunir et Simplifier |
|
|
4x.1/4=8.1/4 (R2): pour n'avoir que 1x( car 4.1/4=1) 1x=8/4 x=2 |
Calculer |
|
|
1er membre: 4.2+1=9 2ème membre: 9 |
Vérifier |
|
|
Une solution: 2 |
Conclure |
Commentaires sur l'exemple 1:
Nous n'avons pas utilisé la première étape: il n'y a aucune parenthèse à enlever ou de fraction à ajouter,...
L'équation donnée est du type de base: ax+b=c où a=4, b=1 et c=9. Nous aurions pu avoir: 1+4x=9 ou 9=4x+1 ou encore 4x-9=-1. Il s'agit de la même équation.
Si vous savez résoudre ce type d'équation, vous êtes prêt à résoudre n'importe quelle équation du 1er degré en x (c'est à dire des équations ne contenant pas de puissances de x).
Nous utilisons d'abord (R1) pour que l'expression contenant x soit isolée dans un membre. Puis nous utilisons (R2) pour calculer la valeur de 1x (écrire 1x ou x est la même chose).
Exemple 2:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etapes |
|
2(x+3)=5x-3 |
2x+6=5x-3 (distribution dans le 1er membre) |
Réduire |
|
2x-2x+6=5x-3-2x (R1): nous rassemblons les inconnues dans le membre qui en contient le plus ( le 2ème ici) en les supprimant dans le 1er. 6=3x-3 6+3=3x-3+3 (R1): pour isoler l'expression 3x (enlever -3 revient à ajouter 3 dans les deux membres) 9=3x |
Réunir et Simplifier |
|
|
9.1/3=3x.1/3 (R2): pour n'avoir que 1x 9/3=1x 3=x |
Calculer |
|
|
1er membre: 2(3+3)=2.6=12 2ème membre: 5.3-3=15-3=12 |
Vérifier |
|
|
Une solution: 3 |
Conclure |
Commentaires sur l'exemple 2:
L'équation donnée ne ressemble pas (à première vue...) à l'équation type. Pourtant dès la troisième ligne de calculs nous sommes parvenus à la manipuler de telle façon que cette fois nous avons bien à faire à une équation du même type que dans l'exemple 1: 6=3x-3 où 6=c, 3=a et -3=b. Il ne reste plus qu'à agir de la même manière...Pour arriver à ce résultat nous avons utilisé deux fois la règle (R1):
*La première fois pour supprimer les expressions contenant x dans le 1er membre (ce qui automatiquement, les fait apparaître dans le second). Pourquoi cette suppression dans le 1er et non le second membre? Tout simplement pour éviter d'obtenir une expression en x avec le signe "moins" (-). Ce qui vous évitera beaucoup d'erreurs lorsque vous résoudrez des inéquations (la méthode est la même mais la règle (R2) est différente).
*La seconde fois pour qu'il ne reste dans le second membre que l'expression en x.
Toutes les étapes sont utilisées. La première étape (Réduire) doit être utilisée pour permettre l'application de la règle (R1). Si vous utilisez (R1) avant toute réduction vous allez au devant de l'échec. Pour cet exemple, la réduction a consisté à distribuer 2 dans le 1er membre. C'est tout mais c'est important pour éviter les erreurs.
Exemple 3:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etapes |
|
4(2-3x)+6x=(x+4)3-10 |
8-12x+6x=3x+12-10 8-6x=3x+2 |
Réduire |
|
8-6x+6x=3x+2+6x (R1): 3 est supérieur à -6 (il y a plus de x dans le second membre) 8=9x+2 (c'est le type de base c=ax+b) 8-2=9x+2-2 (R1): pour isoler 9x 6=9x |
Réunir et Simplifier |
|
|
6.(1/9)=9x.(1/9) (R2) : 1/9 est l'inverse de 9 6/9=x ou 2/3=x |
Calculer |
|
|
1er membre: 4(2-3.2/3)+6.2/3 =4.(2-6/3)+12/3 =4.(2-2)+4 =0+4=4 2ème membre: (2/3+4)3-10 =(2/3+12/3)3-10 =(14/3).3-10 =14-10=4 |
Vérifier |
|
|
Une solution: 2/3 ( et non 4 qui est la valeur de chaque membre lorsque x=2/3) |
Conclure |
Commentaires sur l'exemple 3:
L'étape 1 a été un peu plus longue. Mais vous
remarquez combien elle est nécessaire.
Puis
utilisation de (R1): deux fois, et de (R2). Celle ci n'est généralement
utilisée qu'une seule fois, pratiquement à la fin ( voir
l'exemple suivant pour le cas dans lequel elle est utilisée en premier).
La vérification
a été laborieuse. C'est souvent pour cette raison que nous ne vérifions pas nos
résultats. C'est un tort!
2. L'équation contient des quotients:
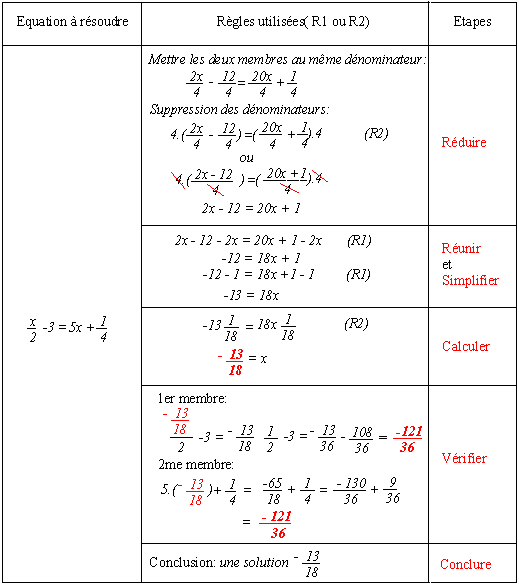
Commentaires:
L'étape de réduction demande une bonne connaissance des règles de calcul sur les quotients. La technique utilisée ici est basée sur la suppression des dénominateurs en utilisant le règle R2, ce qui permet la simplification des quotients (ligne 3 des calculs). Une autre technique est utilisée lorsque l'équation se compose de deux quotients égaux (ou lorsqu'il y a la possibilité de la manipuler pour la ramener à une égalité de deux quotients égaux).
Le reste des calculs est très classique. Attention aux calculs dans la vérification...
Nous avons utilisé ici la règle R2 avant la règle R1. Ce qui est causé par la présence des quotients.
3. L'équation contient des x2:
Exemple 1:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etape |
|
x2 +4x+2=2x+x2 |
Pas utile ici |
Réduire |
|
x2+4x+2- x2=2x+ x2- x2 (R1) 4x+2=2x 4x+2-2x=2x-2x (R1) 2x+2=0 (les x sont dans le membres 1) 2x+2-2=0-2 (R1) 2x=-2 (les x sont seuls dans le membre 1) |
Réunir et Simplifier |
|
|
2x.(1/2)=-2.(1/2) (R2) x= -1 |
Calculer |
|
|
1er membre: (-1)2+4.(-1)+2=1-4+2= -1 2ème membre: 2.(-1)+(-1)2=-2+1= -1 |
Vérifier |
|
|
Conclusion: une solution -1 |
Conclure |
Commentaires:
Si le nombre de x2 est le même dans les deux membres, la règle
(R1) permet de résoudre l'équation en la ramenant au type classique (voir
deuxième ligne de calculs) étudié en quatrième.
Si cette condition n'est
pas vérifiée alors nos connaissances ne nous permettent pas encore de résoudre
ce type d'équation.
Exemple 2:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etape |
|
x.(2x+4)=2x(1+x)+6 |
2x2+4x=2x+2x2+6 |
Réduire |
|
2x2+4x- 2x2=2x+ 2x2+6- 2x2 (R1) 4x=2x+6 |
Réunir et Simplifier |
|
|
4x-2x=2x+6-2x (R1) 2x=6 2x.1/2=6.1/2 (R2) x=3 |
Calculer |
|
|
1er membre: 3(2.3+4)=3(6+4)=3.10=30 2ème membre: 2.3(1+3)+6=6(4)+6=24+6=30 |
Vérifier |
|
|
Conclusion: une solution 3 |
Conclure |
Commentaires: La distribution de la première ligne de calcul fait apparaître un même nombre de x2 dans les deux membres. La règle (R1) règle le problème.
4. Cas particuliers:
Pas de solution:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etape |
|
2x+5=2(x+1) |
2x+5=2x+2 |
Réduire |
|
2x+5-2x=2x+2-2x (R1) 0x+5=2 5=2 !!! |
Réunir et Simplifier |
|
|
|
Calculer |
|
|
|
Vérifier |
|
|
Pas de solution (5 est différent de 2) |
Conclure |
Commentaires:
0x est toujours égal à 0. Mais si nous n'écrivons pas 0x, nous perdons la "trace" de notre inconnue.
A partir de 0x+5=2 nous pourrions continuer par 0x+5-5=2-5 (R1)
Puis: 0x=-3 . Pour calculer x il faudrait utiliser (R2) en multipliant par l'inverse de 0 qui n'existe pas... Nous pouvons donner une autre explication: 0x est toujours égal à 0 quelque soit la valeur donnée à x (et donc jamais égal à -3).
Une infinité de solutions:
|
Equation à résoudre |
Règles utilisées (R1 ou R2) |
Etape |
|
2x+8=2(x+4) |
2x+8=2x+8 |
Réduire |
|
2x+8-2x=2x+8-2x (R1) 0x+8=8 0x+8-8=8-8 (R1) 0x=0 |
Réunir et Simplifier |
|
|
|
Calculer |
|
|
|
Vérifier |
|
|
Il y a une infinité de solutions |
Conclure |
Commentaires:
Nous avons
encore écrit 0x pour garder la lettre désignant l'inconnue. Cette précaution
nous permet de savoir où se trouve notre inconnue.
Quelque soit
la valeur attribuée à « x », zéro fois cette
valeur donne zéro. Toutes les valeurs que nous pouvons donner à x conviennent
comme solution puisque cette fois nous avons bien l'égalité 0=0.
Mettre en équations une situation c'est rechercher toutes les égalités qui traduisent cette situation. En quatrième de collège les situations proposées sont relativement simples. Nous ne parlerons ici que de mises en équation (sans 's') parce que les problèmes choisis pourront se traduire par une seule équation.
Voyez les paragraphes sur la résolution des équations pour plus de précisions sur les calculs dans les équations.
La résolution d'un problème à une inconnue se conduit toujours de la même façon:
Choix de l'inconnue : Soit ... (une lettre désigne la valeur à calculer). C'est ici que nous indiquerons la natrure (entier, décimal,..) de l'inconnue ainsi que les unités éventuelles (mètres, grammes, ..).
Mise en équation: C'est la partie la plus délicate. Elle se traite parfois avec des calculs préliminaires ( pour chaque membre de l'équation à écrire).
Résolution de l'équation: Attention aux erreurs de calculs...
Vérification: Comme pour toute équation.
Conclusion: Rédaction d'une phrase qui rappelle ce qui est calculé, la solution et les unités.
Attention: Ne pas écrire les unités dans une équation.
Situation 1:
|
Deux pommes semblables pèsent 240g. Combien pèse une pomme? |
|
La réponse est évidemment immédiate: 240:2=120g. Mais cette situation peut être mise en équation (pour compliquer les choses!). En effet si nous choisissons x pour désigner la valeur inconnue à calculer (c'est à dire le poids en grammes d'une pomme) nous pouvons écrire: 2x=240 (sans les unités de masse). La résolution de cette équation conduit bien à x=240:2.
Situation 2:
|
La taille de Pierre est 170cm. Pierre est plus grand que Jean de 5cm. Quelle est la taille de Jean. |
|
Toujours aussi simple. Soit x la taille, en centimètres, de Jean (ce qui correspond à la valeur recherchée). pour atteindre la taille de Pierre il faut ajouter 5cm à celle de Jean, ce qui est traduit par: x+5=170 (ne pas écrire les unités). La résolution de cette équation conduit à x=170-5. Conclusion: la taille de jean est 165cm.
Situation 3:
|
Dans le sac de Marie il y a 2 pommes semblables (encore!) et une boîte de conserve sur laquelle est noté le poids: 250g. Marie sait que l'ensemble pèse 630g (nous négligeons le poids du sac...). Evidemment nous voudrions connaître le poids de l'une des pommes! |
|
Encore très simple, quoique...! Choix de l'inconnue: facile, soit « x » le poids en grammes d'une pomme.
Mise en équation: il s'agit d'écrire une égalité. Si nous connaissons le poids d'une pomme (c'est à dire x) nous pouvons calculer le poids de 2 pommes (donc:2x). Dans le sac il y a les deux pommes mais aussi une boîte de conserve dont nous connaissons le poids: 250g. Le sac pèse donc 2x+250. L'énoncé nous donne justement la masse totale égale à 630g, c'est donc que:
2x+250=630
La rédaction de la solution est:
Soit x le poids en grammes d'une pomme.
2x+250=630
2x+250-250=630-250 (R1) (voir résolution des équations)
2x=380
2x.(1/2)=380.(1/2) (R2)
x=190
Vérification:
1er membre: 2×190+250=630
2ème membre: 630 (donné par l'équation)
Conclusion: une pomme pèse 190g (les unités sont ici obligatoires!).
Situation 1:
|
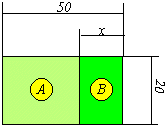
Un terrain rectangulaire est partagé en deux parties rectangulaires A et B. Calculer la valeur de x pour que le périmètre de la partie A soit le double du périmètre de la partie B. Les dimensions sont données en mètres. |
|
Choix de l'inconnue: Nous n'avons pas vraiment le choix!
Soit x la largeur en mètres de la partie B
Mise en équation: Nous devons calculer le périmètre de chaque partie et écrire que le périmètre de A (désigné ici par P) est le double de celui de B (désigné par p). Les lettres P et p ne sont pas nécessaires dans votre rédaction. Elles ne servent ici qu'à expliquer le raisonnement.
Périmètre de A: P=(largeur+longueur).2 où largeur est 20m et longueur=50-x. D'où: P=(20+50-x).2=(70-x).2=140-2x
Périmètre de B: p=( largeur+longueur).2 où largeur est x et longueur=20. D'où: p=(x+20).2 ou 2x+40
L'équation est donc: P=2p ou 140-2x=(2x+40).2
Résolution de l'équation: Vous devriez trouver x=10
Vérification:
1er membre: 140-2.10=140-20=120
2ème membre: (2.10+40).2=60.2=120
Conclusion: Pour que le périmètre de la partie A soit le double de celui de la partie B il faut que x (ou: la largeur de B) soit égale à 10m.
Situation 2:
Certaines situations peuvent faire penser que deux lettres sont nécessaires pour désigner les inconnues. Lisez bien l'énoncé suivant et essayez de trouver une donnée commune aux deux inconnues:
|
Pierre achète 25 crayons de deux types A et B. Le type A coûte 6€, le type B coûte 8€. Il a dépensé en tout 170€. Combien y a-t-il de crayons de chaque type? |
Avez vous trouvé? En effet les 25 crayons comprennent les deux types. Si nous connaissons le nombre de crayons de type A (ou B) un petit calcul nous permet d'obtenir le nombre de crayons de l'autre type. Il suffit donc de calculer le nombre de crayons de l'un des deux types (A ou B, peu importe).
Choix de l'inconnue: Soit x le nombre (entier) de crayons de type A.
Mise en équation:
Le nombre de crayons de type B est 25-x.
La somme dépensée pour les crayons de type A est 6x (x crayons à 6 € ).
La somme dépensée pour les crayons de type B est (25-x).8 ( 25-x crayons à 8 €);
La somme totale est donc: 6x+(25-x).8 mais aussi 170 € (donnée du problème).
L'équation est: 6x + (25-x) .8 = 170
Résolution: Nous obtenons x=15 (si nous avions obtenu un nombre non entier, nous n'aurions eu aucune solution au problème, même si il y avait eu une solution à l'équation)
Vérification: N'oubliez pas: 1er membre...2ème membre...
Conclusion: Il y a 15 crayons de type A et 25-15=10 crayons de type B (voir ligne 1 de la mise en équation).