WARMATHS : Conseils A remanier

1. Introduction 2. Comment lire les données? 3. A quoi sert la figure? 4. Comment répondre aux questions? 5. Qu'est ce qu'un théorème? 6. Comment trouver le "bon" théorème? 7. Comment utiliser ce théorème? 8. Comment rédiger son devoir? 9. Conclusion et téléchargement.

1. Introduction:

Je ne prétends pas détenir le secret de la réussite en Mathématiques. J'ai enseigné la géométrie en 4ème et 3ème pendant de nombreuses années . Ce qui m'a permis d'analyser en collaboration étroite avec quelques collègues, les causes des échecs fréquents rencontrés dans l'apprentissage de la géométrie. La méthode de travail que nous avons élaborée ensemble nous a prouvé son efficacité dans nos classes et dans les résultats aux examens du brevet des collèges. Vous trouverez peut-être ici une solution aux difficultés que vous rencontrez dans l'apprentissage de la Géométrie en particulier, des Mathématiques en général.

L'algèbre vous paraît bien sûr plus facile. C'est une erreur de croire cela: ce n'est pas le calcul algébrique qui est plus facile mais, le vocabulaire utilisé fait penser que nous sommes en terrain connu parce que composé de mots de tous les jours. En fait nous sommes en terrain miné !

Exemple: quel est le plus grand entier relatif inférieur à -2,5 ?

Il n'y a dans cette phrase que des mots connus. Le nombre -2,5 est un décimal négatif qui est une notion que vous devez connaître. Savoir aussi que -3, -4, -5,.. sont inférieurs à -2,5 ( pas -2 qui est supérieur à -2,5 !) et que ce sont des entiers (relatifs). Alors la réponse est...? -3 bien sûr.

Pas si simple finalement... Il vous fallait connaître certaines définitions associées à des mots connus tels que "plus grand", "entier",... ainsi que certaines notions telles que "entier relatif", "ordre dans l'ensemble des nombres entiers relatifs",... Vous avez été amené à RAISONNER comme nous pouvons le faire en Géométrie. Seuls les mots et les notions à connaître sont différents . La manière de les manipuler est la même. A partir de faits connus que nous assemblons, nous déduisons des éléments qui étaient inconnus. Chercher la solution d'un problème mathématique (et notamment géométrique) ressemble fort à une enquête policière! Il y a les indices et les outils pour manipuler ces indices.

2. Comment lire les données d'un problème?

Bien évidemment, il faut savoir lire! Mais qu'est ce que "savoir lire un énoncé"? Ce n'est pas forcément "lire vite" et ne rien comprendre à ce que nous avons lu... Ce n'est pas non plus arrêter la lecture dès la première question et se mettre à écrire quelque chose qui ressemble à une réponse. Neuf fois sur dix, celle-ci sera soit fausse, soit incomplète ou carrément à côté. De cette façon nous n'arriverons à rien...

La méthode de lecture que je vous propose est moins rapide, bien sûr, mais vous arriverez beaucoup plus sûrement à un résultat...si vous le désirez. La voici:

1. Lire l'énoncé en entier (même long, je dirai même: surtout lorsqu'il est long). Pendant cette lecture vous notez sur une feuille de papier les mots ou expressions que vous ne connaissez pas ou dont vous n'êtes pas sûr d'en bien comprendre le sens.

2. Rechercher dans le Répertoire les mots ou expressions que vous avez notés. Si vous exécutez ce travail chaque fois que vous avez un problème à résoudre, la feuille de papier finira par rester blanche (parce que vous mémorisez et comprenez de mieux en mieux).

3. Relire l'énoncé en entier une ou plusieurs fois et construisez votre figure (en géométrie, la plupart des problèmes demande à être illustré par une figure, à moins que celle-ci ne soit déjà construite dans votre livre). Vous devez maintenant avoir une meilleure idée de la situation qui est décrite, des indices qui vous sont fournis et des faits qu'il vous faut prouver. Vous avez même, peut-être, déjà une idée des outils (les théorèmes) qu'il vous faut utiliser. Certaines questions vous mettrons même sur la voie de la découverte (voilà pourquoi il vous faut tout lire).

4. Relire chaque question et y répondre correctement.

En résumé: Tout lire ** S'informer avec le répertoire ** Tout relire ** Relire et répondre question par question.

3. A quoi sert la figure dans la résolution d'un problème?

Une figure propre et tracée avec précision vous apportera une aide précieuse dans la recherche de la solution. Pour cela il faudra vous contraindre à effectuer d'abord une figure à "main levée", c'est à dire sans règle ni compas ou équerre.

Cette figure sera probablement fausse mais elle vous fera réfléchir sur la façon de tracer la figure définitive. Par exemple: elle vous permettra d'éviter les cas particuliers, les droites qui se coupent en dehors de votre page. Elle vous fera découvrir aussi les erreurs d'interprétation (droites parallèles au lieu de sécantes par exemple) ou vous fera abandonner une idée préconçue (par exemple: un point que vous teniez absolument à placer au milieu d'un segment alors que rien de spécial n'était dit à son sujet...).

Dès que votre figure est tracée vous pouvez l'enrichir avec les indices que vous avez découvert dans l'énoncé jusqu'au niveau de la première question. C'est à dire: repasser en vert les droites parallèles, indiquer par un petit carré vert les angles droits ou le fait que deux droites sont perpendiculaires, tracer en vert des petits traits qui indiquent l'égalité de deux angles (si vous êtes informé de leur mesure écrivez la sur le trait) ou de deux segments (mesure à écrire dessus, en petit).

Au fur et à mesure que vous avancez dans le problème, portez sur la figure, en vert, les indices que vous avez découverts. L'observation de cette figure vous fera découvrir, avec un peu d'entraînement, des configurations compatibles avec certains théorèmes. Avant d'utiliser un théorème vérifiez bien que la partie en vert (les hypothèses = les indices) derrière le "SI" est illustrée sur votre figure avec la même couleur. Ceci vous assure que vous pouvez utiliser ce théorème.

Sur votre figure vous aurez parfois "l'impression" que des droites sont concourantes (se coupent en un même point) ou qu'un point est le milieu d'un segment... Méfiez vous! N'en croyez pas vos yeux! Essayez de démontrer le fait et si vous n'y arrivez pas, refaite une autre figure avec d'autres mesures, des points placés autrement,..

4. Comment répondre aux questions d'un problème?

Les questions d'un problème sont posées dans un certain ordre. Cet ordre est très important. Mais vous n'êtes pas obligé, dans votre recherche, de le respecter. Ce qui signifie que vous pouvez rédiger la solution de la question 3, par exemple, avant celle de la question 2, ou même de la question 1. Si vous êtes en devoir surveillé, n'oubliez surtout pas d'indiquer, par son numéro, de quelle question il s'agit. En devoir surveillé, je vous conseille de rédiger le moins possible au brouillon, l'entraînement du travail à la maison doit vous permettre cela. Si vous êtes sur un devoir ou un exercice à étudier à la maison, rédigez la solution au brouillon. Vous ne présenterez les solutions, dans l'ordre des questions, que lors de la mise au propre.

Attention cependant à la remarque suivante: vous ne pouvez pas utiliser le résultat de la question 4, par exemple, pour démontrer une question précédente (les questions 1, 2 ou 3 dans cet exemple). En effet, ce qui n'est pas connu à la question 4 ne l'est pas non plus à la question 3 qui vient avant! C'est une question de chronologie (ordonnancement dans le temps: "vous ne pouvez pas récolter avant d'avoir semé" ou "vous devez semer avant de récolter", deux façons de dire la même chose).

Mais rien ne vous empêche d'utiliser les découvertes que vous avez faites à la question 3 pour traiter la question 4. Si vous n'avez pas trouvé la solution de la question 3 vous pouvez quand même en utiliser le résultat pour traiter la question 4, ou 5,..: vous agissez comme si vous récoltiez ce que quelqu'un d'autre a semé. Ce qui vous permet de traiter les questions dans n'importe quel ordre en faisant bien attention à respecter la remarque ci-dessus.

Les conseils pour la rédaction des solutions sont donnés dans les paragraphes suivants. Mais sachez tout de suite, que ces rédactions ne doivent contenir d'autres mots que ceux contenus dans les théorèmes utilisés à l'exception du "SI" qui doit être remplacé par le mot "Comme". Tout autre formulation n'est que blabla inutile. N'ayez pas peur des répétitions, vous n'écrivez pas un poème! Bien que certaines démonstrations, par leur rigueur et leur clarté, ont de quoi charmer l'esprit...

5. Qu'est ce qu'un théorème?

Les théorèmes sont les outils utilisés pour manipuler les renseignements (les hypothèses = les indices de notre enquête) donnés par l'énoncé du problème (qui décrit la situation dans laquelle se trouve le détective).

Ils se présentent toujours de la même manière:

SI .--------------( en vert )---------------------------------

ALORS ---------------(en rouge)--------------------------

Ce qui est énoncé après le "SI" représente le(s) hypothèses(s), c'est à dire les faits connus. Ces faits nous les connaissons soit parce qu'ils sont exposés dans l'énoncé du problème, soit parce que nous les avons déjà établis grâce à d'autres théorèmes, ou dans la solution de questions précédentes.

Ce qui est énoncé après le "ALORS" représente un nouvel élément, un nouvel indice qui a été prouvé dans une situation identique.

Démontrer un théorème c'est donc forger un outil en prouvant que dans une situation donnée( SI....) il est permis d'affirmer un fait nouveau (ALORS....). Les démonstrations des théorèmes se trouvent dans les livres de cours ou plus simplement dans votre cahier de cours. Vous trouverez de nombreuses démonstrations de théorèmes importants sur ce site, à l'occasion de l'exposé des cours ou de révisions. Ces démonstrations sont d'excellents exemples de rédaction et de réflexion.

6. Comment trouver le "bon "théorème? (important: à lire et à relire)

Le plus difficile est de trouver le théorème qui convient. Le plus rapide est de rechercher dans sa mémoire. Mais pour cela il faut qu'il y ait quelque chose dans cette mémoire. L'excuse la plus commune est: "je n'ai pas de mémoire", ce qui règle le problème ( "pas besoin de chercher puisque je n'ai rien dans ma mémoire"). Celui qui dit cela sait donc qu'il doit la remplir cette mémoire. Cela exige de lui un effort particulier, d'autant plus grand que sa mémoire est vide! Plus elle sera remplie, plus il lui sera facile de l'agrandir. Ce sont donc les premiers efforts qui coûtent le plus. L'ennui c'est que ce sont justement ces premiers efforts qui le rebutent et lui font baisser les bras. Si celui là savait comme tout devient beaucoup plus facile après...

Pour vous aider à nourrir votre mémoire n'hésitez pas à aller voir dans le Répertoire dès que vous butez sur un terme, ou une notion, mal connu. Le plus simple, cependant, est d'aller voir dans les Fiches. Il y en a dix. Il ne s'agit pas de les afficher (dans le cadre du bas) toutes à tour de rôle, en espérant "tomber" sur un théorème qui "semble" convenir! La façon de faire suivante est beaucoup plus rapide (malgré les apparences) et plus fiable:

1 -Lisez bien la question qui est posée: elle indique clairement ce que vous devez démontrer.

2 -Cliquez dans le sommaire (cadre de gauche) sur "Fiches"; Dans le tableau affiché dans le cadre du bas (agrandissez ce cadre si nécessaire) choisissez la fiche qui se rapporte à la question.

Exemple: soit la question "Montrez que (d1) et (d2) sont parallèles." , pas de doute vous devez choisir la fiche intitulée "Pour démontrer que des droites sont parallèles" de code DPAR et de numéro 5; un clic sur ce code vous amène la fiche dans le cadre du bas.

3 -Dans cette fiche il vous faut choisir le théorème qui convient: vous devez rechercher en priorité le théorème dont les hypothèses (en vert) sont connues pour la question que vous traitez.

· Si vous en trouvez un qui respecte cette condition, vous avez trouvé le "bon" théorème. Il ne vous reste plus qu'à le rédiger.

· Sinon il est inutile d'aller voir tout de suite dans une autre fiche. Il vaut mieux réfléchir un peu: voyez le point suivant...

4 -Si vous n'avez pas trouvé de théorème qui convient, c'est que vous n'êtes pas en possession de toutes les hypothèses. Ce qui signifie que la question posée demande deux théorèmes ou même plus pour sa résolution. Vous devez donc démontrer ce qu'il vous manque! Mais comment trouver? La plupart du temps, en comparant les parties de votre figure à celles qui accompagnent chaque théorème dans les fiches, vous arriverez à "deviner" la propriété à démontrer. Une fois que vous en êtes là, vous devez poursuivre votre travail de recherche en recommençant au point 2 ci-dessus, pour trouver à nouveau un "bon" théorème. Ce qui peut vous amener à en chercher un troisième,... Dans ce cas, c'est que la question posée est vraiment difficile à traiter, vous n'en aurez que plus de mérite si vous en trouvez la solution.

5 -Rédigez la solution de la question en reprenant les théorèmes dans l'ordre inverse où vous les avez découverts (lorsqu'il y en a plusieurs!).

Cette façon de faire est illustrée ci-dessous. Les nombres indiquent les points décrit ci-dessus.

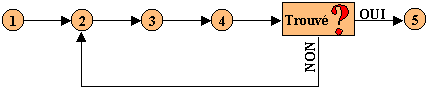
7. Comment utiliser un théorème?

Vous avez trouvé le "bon" théorème. Bien!

Il faut maintenant le mettre en forme. Rien de plus simple. Reprenons la question "Montrer que (d1) et (d2) sont parallèles." et supposons que les hypothèses en votre possession sont "EFGH parallélogramme avec E et F sur (d1) et G et H sur (d2)". Il vous faut donc le théorème:

SI un quadrilatère est un parallélogramme

ALORS ses côtés opposés sont parallèles.

Il y a évidemment d'autres théorèmes pour démontrer que des droites sont parallèles, mais celui ci est tout à fait adapté à nos hypothèses. Pour le rédiger il faut mettre à jour deux choses:

· remplacer le "SI" par "Comme" : en effet, le théorème utilise le conditionnel ( SI... signifie "à condition que les hypothèses suivantes soient vérifiées...") pour affirmer (ALORS....) une nouvelle propriété. Dans la rédaction, nous savons que les conditions sont vérifiées (nous avons justement pris beaucoup de précautions pour cela!) et par conséquent nous n'avons plus besoin du "SI" et nous affirmons les hypothèses en écrivant "Comme...".

· remplacer les objets et leur nom( points, droites, quadrilatères, cercles, angle, ABCD, A,...) utilisés dans le théorème par les objets, avec leur nom, effectivement utilisés dans le problème. Dans notre exemple il faut remplacer: "un quadrilatère" par "EFGH" ou "le quadrilatère EFGH", "les côtés opposés" par "les côtés opposés (EF) et (GH)".

Ce qui donne la rédaction suivante:

Comme le quadrilatère EFGH est un parallélogramme

Alors les côtés opposés (EF) et (GH) sont parallèles.

Vous devez remarquer sûrement deux choses: les couleurs sont abandonnées (elles ne servent que pour la recherche) et les objets (d1) et (d2) n'apparaissent pas dans cette rédaction. Ce qui est gênant...et expliqué au paragraphe suivant.

8. Comment rédiger son devoir?

Vous avez trouvé les "bons" théorèmes et vous les avez mis en forme. C'est presque parfait. Reste à conclure chacun d'eux pour répondre parfaitement aux questions. Reprenons l'exemple des paragraphes précédents: nous devons démontrer que (d1) et (d2) sont parallèles. Nous avons démontré que (EF) et (GH) sont parallèles et nous savons que E et F sont sur (d1) et que G et H sont sur (d2). Il suffit de transformer (EF) en (d1) et (GH) en (d2) pour écrire finalement:

Comme le quadrilatère EFGH est un parallélogramme

Alors les côtés opposés (EF) et (GH) sont parallèles.

Conclusion: (EF) et (d1) sont une même droite, de même pour (GH) et (d2) . Les droites (d1) et (d2) sont donc parallèles.

Certaines questions vous amènent parfois à utiliser plusieurs théorèmes. Vous devez les rédiger tous comme montré au paragraphe précédent mais vous ne concluez qu'une fois, après le dernier théorème, et dans le sens imposé par la question.

Vous pouvez rédiger les solutions aux questions sans suivre obligatoirement l'ordre de ces questions mais respectez bien ce qui est dit au paragraphe 4.

9. Conclusion:

J'ai essayé d'être le plus clair possible. Ce qui m'a entraîné, peut-être, à devenir parfois un peu long et même franchement ennuyeux. Veuillez m'en excuser. Cependant je vous invite à revenir de temps en temps sur ce document, pour bien savoir comment vous y prendre avec un problème de géométrie. Vous adapterez sûrement cette méthode à vos habitudes personnelles de travail, si vous en avez, et à votre tempérament. Ce qui vous aidera par la suite dans toutes vos études, et pas seulement qu'en Mathématiques!

.