WARMATHS

La Rotation

I. Introduction:

La roue ne fut utilisée (d'après ce que nous en savons...) qu'à partir du quatrième ou cinquième millénaire avant notre ère (il y a donc de 6 à 7 mille ans...). C'est l'invention de l'essieu qui a permis d'utiliser la roue pour le transport, pour la construction de machineries de plus en plus complexes.
La notion de rotation en découle tout naturellement. Il s'agit d'un déplacement dans le plan qui, à tout point, fait correspondre un point, en "tournant" autour d'un point central, comme la roue autour de son essieu.

II. Définition:

· Sens de rotation

· Construction de l'image d'un point.

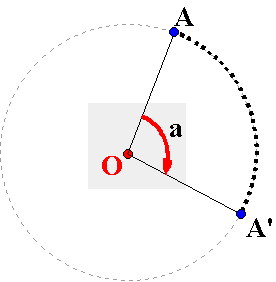
Soit un point O. Le point A est déplacé par une rotation autour de O lorsqu'il décrit un arc de cercle de centre O, de rayon OA. Son image A' est le point extrémité de cet arc de cercle.
Dans le cadre grisé de la figure ci dessous, se trouve l'essentiel de la définition d'une rotation.

Une rotation est un déplacement dans un plan

- autour d'un point appelé centre de la rotation.
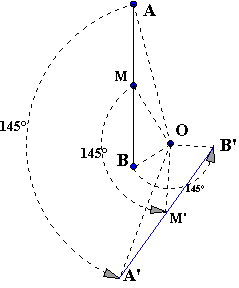
- d'un angle appelé angle de la rotation.
- dans le sens des aiguilles d'une montre (ou le sens inverse).

La rotation illustrée par la figure ci dessus est notée R(O, a) où O est son centre et a son angle. La définition ci dessus implique que l'image d'un point, par une rotation, est un point.
Le centre de rotation est un point invariant (son image est lui même)
Pour des valeurs de l'angle de rotation de 0°, 180° (-180), 360° (-360°) les images occupent des positions particulières. Pour ces valeurs voir "Cas particuliers".

Remarque: dans un plan il y a deux sens de rotation possibles:
- dans le sens des aiguilles d'une montre : dans ce cas l'angle est noté négativement de 0 à -360° (ex: rotation d'angle -60°).
- dans le sens contraire des aiguilles d'une montre. Ce sens est appelé sens trigonométrique. Dans ce cas l'angle de rotation est noté positivement de 0 à 360° (ex: rotation d'angle 45° ou +45°).

Construction de l'image d'un point:
Pratiquement, une rotation est donnée à l'aide de son centre, d'un point et de son image: voir le paragraphe concernant les constructions.

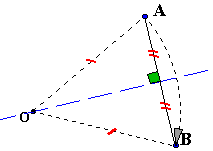
Propriété du centre:

Soit la rotation de centre O, qui amène le point A sur le point B.
La médiatrice de [AB] passe par le centre de rotation. En effet:
Comme B est l'image de A par la rotation de centre O alors OA=OB
Comme OA=OB alors O appartient à la médiatrice de [AB].(ALI n°6a)
Par ailleurs, cette médiatrice est perpendiculaire au segment qui joint le point A et son image, et passe au milieu de ce segment (propriété fondamentale d'une médiatrice (DPER n°2))

III Cas particuliers:

Des valeurs particulières de l'angle de rotation conduisent à des situations très particulières.
Soit O le centre de rotation:
- Angle de rotation égal à 0° ou 360° ou -360°: cette rotation fait correspondre chaque point d'une figure à lui même. La figure est invariante point par point.
- Angle de rotation égal à 180° ou -180°:

Si le point A a pour image A' alors OA=OA' et l'angle AOA' est plat (=180°).
Comme les points A, O et A' sont alignés et OA=OA' alors O est le milieu de [AA']. (MIL n°01)Et ceci quelque soit le point A.
Nous retrouvons la propriété fondamentale des symétries centrales.
Pour un angle de rotation de 180° (ou -180°) nous obtenons une symétrie centrale de centre O

IV. Propriétés:

· Conservation de la distance

· Conservation des alignements

· Image d'une droite (demi droite, segment)

· Image du milieu d'un segment

· Conservation des angles

· Conservation des aires

1. Conservation de la distance:

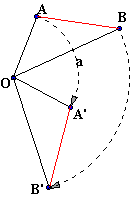
Sur la figure ci contre, les points A et B ont pour images A' et B' par la rotation de centre O et d'angle a.
Nous pouvons démontrer que AB=A'B'. (voir la démonstration)

Les rotations conservent les distances.

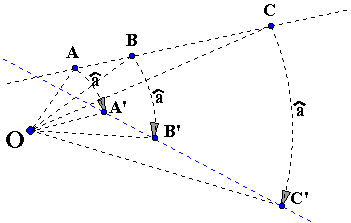
2. Conservation des alignements:
Rappels: si A, B et C,dans cet ordre, sont alignés alors AB+BC=AC. (cas particulier des inégalités triangulaires)
et sa réciproque: Si AB+BC=AB alors A, B et C sont alignés (ALI n°05).

Soient les points alignés A, B et C et leurs images A', B' et C' par la rotation de centre O et d'angle a.
Comme les rotations conservent les distances alors AB=A'B', BC=B'C' et AC=A'C'.
Comme A, B et C sont alignés alors AB+BC=AC.
Si nous remplaçons AB, BC et AC par les valeurs égales, respectivement, A'B', B'C' et A'C', nous obtenons A'B'+B'C'=A'C'.
Comme A'B'+B'C'=A'C' alors A', B' et C' sont alignés. Ce qui prouvent que:

Les rotations conservent les distances

3. Image d'une droite:
Soit la droite (d) et la rotation de centre O et d'angle a.
Soit M un point quelconque de (d). M peut occuper une infinité de positions sur (d). Toutes ces positions sont alignés. A chacune de ces positions correspond une image P'. Comme les rotations conservent les alignement alors toutes les positions de P' sont alignés. Donc lorsque P décrit (d), P' décrit aussi une droite.

L'image d'une droite par une rotation est une droite.

Conséquence:
Une demi droite [Ax), un segment [AB] sont des morceaux de droite. Leurs images sont donc respectivement une demi droite dont l'origine est l'image de l'origine A et un segment. De plus comme les rotations conservent les distances l'image du segment a la même longueur. Donc:

L'image d'une demi droite d'origine A est une demi droite d'origine le point image de A.
L'image d'un segment [AB] est un segment de même longueur.

4. Image du milieu d'un segment:

Soient le segment[AB] et son milieu M.
A' et B' sont les images de A et B par la rotation de centre O et d'angle a.

Comme M est le milieu de [AB] alors A, M et B sont alignés et AM=MB.(ALI n°04) Comme les rotations conservent les alignement alors les images A', B' et M' sont alignés. Comme les rotations conservent les distances alors AM=A'M', MB=M'B'. Donc A'M'=M'B'. Comme A', M' et B' sont alignés et A'M'=M'B' alors M' est le milieu de [A'B'].(MIL n°01)
L'image du milieu d'un segment est le milieu de l'image du segment

5. Conservation des angles:

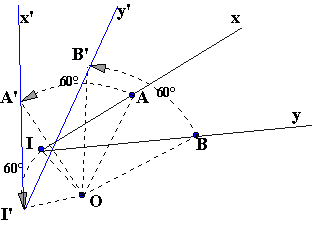
Soit l'angle xIy. Par la rotation (O,a) les côtés [Ix) et [Iy) ont pour images les demi droites [I'x') et [I'y'). (voir 3° ci-dessus). Soient les points A et B, respectivement, sur [Ix) et [Iy). Leurs images sont les points A' et B', respectivement, sur [I'x') et [I'y').
Comme les rotations conservent les distances alors les triangles ABI et A'B'I' ont leurs trois côtés de même longueur. Les triangles ABI et A'B'I' sont donc superposables et leurs trois angles sont donc égaux. Notamment les angles xIy et x'I'y'. Donc:

Les rotations conservent les mesures des angles.

6. Conservation des aires:
Les rotations conservant les distances, les angles et les alignements, toute figure est superposable à sa figure image Donc l'aire d'une figure est égale à l'aire de la figure image.

Les rotations conservent les aires.

V Constructions:

Il s'agit ici de constructions d'images par une rotation de centre O et d'angle a (variable selon la construction).

· 1. Image d'un point: l'image d'un point est un point
Soient les points A, B et C. Le point A' est l'image de A par la rotation de centre O et d'angle +45°. Construire les images B' et C' de B et C dans la même rotation.
Les outils à utiliser sont: la règle, le compas et le rapporteur. Pour ce dernier, si vos souvenirs sont flous, cliquez ici.

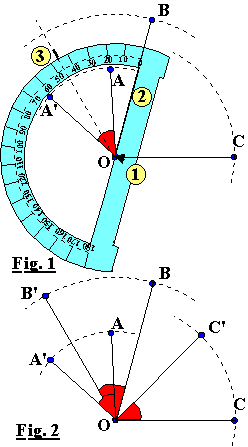
Pour construire A': (fig 1)
Tracer [OA], [OB] et [OC].
Attention: l'angle de la rotation est noté positif, la rotation est donc dans le sens trigonométrique (sens inverse des aiguilles d'une montre).. Avec le compas tracer un arc de cercle de centre O dans le sens trigonométrique, en partant de A. Profitez en pour tracer aussi les arcs partant de B et de C.
Avec le rapporteur reporter un angle de 45° de sommet O et de côté (OA). Le deuxième côté de cet angle coupe l'arc de cercle en A', image de A dans cette rotation.

Pour les images de B et C: (fig. 2)
Avec le rapporteur reporter un angle de 45°, centre du rapporteur en O, côté de départ (OB), puis (OC). Les seconds côté de ces angles coupent les arcs en B' et C'.

Utilisation du rapporteur: construction de B'.

1. Placer le centre du rapporteur sur O.
2. Aligner le diamètre du rapporteur avec (OB).
3. Compter 45° et tracer un petit trait à partir du bord du rapporteur. Tracer la droite qui passe par ce trait et O.

·
2. Image d'une droite: l'image d'une droite est une droite

· Soit une droite (d). L'angle de rotation est -60. Construire (d'), image de (d) .
Il suffit de choisir deux points A et B sur (d) et d'en déterminer les images A' et B'.
La droite image est (A'B').

· 3. Image d'un angle: l'image d'un angle est un angle de même mesure

· Soit l'angle xIy. L'angle de rotation est 30°. Construire uI'v, image de xIy.
Choisir sur chacun des côtés un point : A et B par exemple. Déterminer les images I' du sommet I ainsi que les images A' et B' de A et B. Joindre ensuite I' à A' et I' à B' et prolonger.
Attention: ce type de construction demande beaucoup de soin. La figure obtenue n'est pas toujours très lisible; il suffit, parfois de modifier la position des points A e/ou B.

· 4. Image d'un cercle: l'image d'un cercle est un cercle de même rayon

· Soit le cercle de centre I et de rayon 4cm. l'angle de rotation est quelconque.

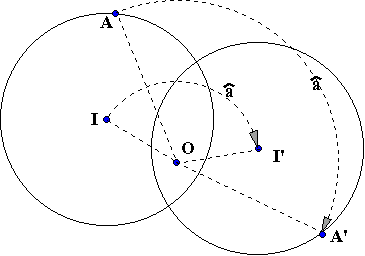
Il suffit de déterminer l'image I' du centre I et de tracer le cercle de centre I' et de même rayon. Il n'est pas utile dans cette construction, de déterminer l'image d'un point du cercle bien que ce ne soit pas interdit !
Dès que l'image du cercle est obtenue, le placement de l'image A' d'un point A du cercle donné est très souvent la cause d'erreur. Vérifiez bien que l'angle de rotation est respecté.
Remarque: un cercle est invariant par toute rotation dont le centre est le centre du cercle

VI Problème résolu:

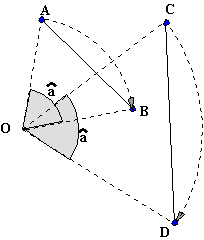
Soient les points O, A, B, C et la rotation Rot de centre O qui amène le point A sur B. Soit le point D l'image de C par Rot.

1. Montrer que les médiatrices de [AB] et [CD] se coupent en O.
2. Montrer que l'image de (AC) par Rot est (BD).

Soit E le point de (AC) tel que (OE) perpendiculaire à (AC), et F, point de (BD) tel que (OF) perpendiculaire à (BD). Les droites (AC) et (BD) se coupent en I.

3. Montrer que l'image de E par Rot est F.
4. Montrer que O appartient à la bissectrice de l'angle EIF.
5. Montrer que l'angle AIB est égal à l'angle AOB.

Remarque: l'angle AIB est l'angle formé par la droite (AC) et par son image (BD). Cet angle est égal à l'angle de la rotation. Ceci est vrai quelque soit une droite et son image par une rotation.
(voir la solution).