|
WARMATHS |
Bissectrice |
·
Définitions.
·
Construction de la bissectrice d'un angle.
·
Cas particuliers.
Définitions:
La bissectrice d'un angle est son axe de
symétrie.
La
bissectrice d'un angle le partage en deux angles adjacents de même mesure.
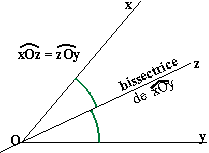
Le point O est le sommet de l'angle. Les demi
droites [Ox) et [Oy) en
sont les côtés.
Un angle est mesuré à l'aide d'un rapporteur
d'angle dans diverses units (le degré étant le plus
utilisé au collège).
Propriétés:
(Note: ce qui doit être connu est noté en
vert, ce qui peut être démontré est noté en rouge)
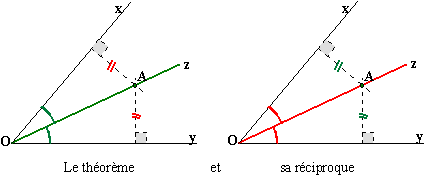
Si un point appartient à la bissectrice d'un angle
Alors ce point est équidistant des côtés de cet angle.
et le théorème
réciproque (échange des couleurs: de vert vers rouge et vice-versa):
Si un point est équidistant des
côtés d'un angle
Alors ce point appartient à la
bissectrice de cet angle.
Construction de la bissectrice d'un
angle:
Données: angle de sommet 0 et
de côtés [Ox) et [Oy)
Construire
la bissectrice de cet angle.
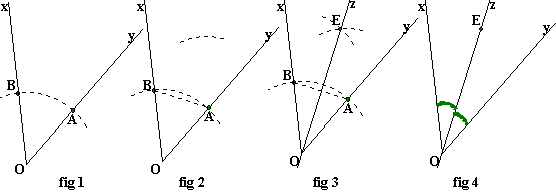
Fig 1: avec le compas pointé
en O (le rayon est quelconque) tracez un arc de cercle qui coupe les côtés en A
et B.
Fig 2: avec le compas
pointé en A (le rayon est quelconque, pas forcément égal au premier) tracez un
arc dans l'intérieur de l'angle.
Fig 3: avec le compas
pointé en B et le même rayon que ci-dessus,
tracez un arc qui coupe l'arc de la figure 2 au point E.
Fig 4: La droite (OE)
est la bissectrice demandée.
Commentaires:
- La figure 1 montre comment
obtenir un segment [AB] dont les extrémités sont sur les côtés de l'angle
et tel que le sommet O soit équidistant des extrémités A et B (la distance
est le rayon choisi). Comme O est équidistant de A et B alors O appartient
à la médiatrice de [AB] et OAB est isocèle de sommet principal O.
- Les figures 2 et 3 montrent
comment obtenir un second point E de la médiatrice de [AB] (EA=EB=rayon
des deux arcs de cercle). Tracer la bissectrice (OE) c'est donc tracer
l'axe de symétrie du segment [AB] et du triangle isocèle OAB. Comme la
droite (OE) est l'axe de symétrie de l'angle BOA alors (OE) est la
bissectrice cherchée.
Cas particuliers:
Bissectrices d'un triangle: les trois
bissectrices d'un triangle sont concourantes en un point qui est le centre du
cercle inscrit dans ce triangle.
Remarque: Dans un triangle isocèle, la
bissectrice de l'angle dont le sommet est le sommet principal, est aussi
hauteur, médiane et médiatrice du côté opposé.
Bissectrices des angles d'un carré et d'un losange: les bissectrices de
ces angles sont les diagonales de ces quadrilatères.
Bissectrices de deux angles supplémentaires et adjacents:
Sur la figure ci-dessous les angles xOz et zOy sont supplémentaires
et adjacents, ce qui entraîne que xOy est un angle
plat (il mesure 180°). Nous avons représenté en traits pointillés les
constructions des bissectrices (Ou) et (Ov) (nous
nous sommes limités ici aux demi-droites). Nous vous conseillons de les faire
sur une feuille de papier et de compléter la démonstration commencée sous la
figure.
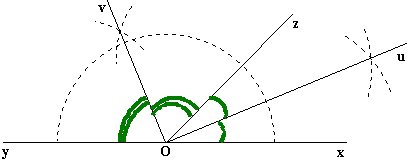
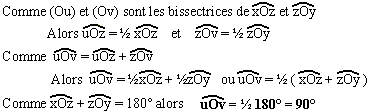
Conclusion: Les
bissectrices de ..... sont .....