CORRIGE du devoir sommatif
:
CONTROLE :
a) un « tableau de variation » est le représentant d’une fonction si …. ?
Un tableau de variation est le représentant d ' une
fonction si à une valeur de (x) correspond une seule ( au plus ) valeur de
"y".
b) Que désigne le mot « variable » ?
une variable est une lettre qui peut prendre
différentes valeurs.
Fin du rappel :
1°) Donnez le modèle mathématique de l’équation représentant la fonction linéaire.
L’équation est de la forme y = a x
2°) Que peut-on représenter
à partir d’une équation
représentant la fonction linéaire ?
on peut représenter à partir d’une équation :
un tableau de proportionnalité ;un graphe ; une représentation
graphique.
3°) Soit la notation
« ax » , comment nomme - t - on les facteurs ?
« a » désigne le coefficient directeur ,
ou de proportionnalité de la droite.
« x » représente la variable.
4°) Donnez la forme des couples qui forment eux mêmes le graphe de la
fonction linéaire.
Forme des couples ( x1 ; ax1)
5°) Donner forment du
graphe de la fonction linéaire. ( donner les deux couples particuliers)
le Graphe de la fonction linéaire est de la
forme :
G = {( 0 ; 0 ) ; ( x1 ;
ax1) ; (x2 ;ax2 ) ; ......... }
Avec comme les deux
couples particuliers :
( 0 ; 0 ) et ( 1 ; a )
6°) Représenter le tableau de
« proportionnalité ; précisez ce qu’il « contient ».
Modèle
de tableau de proportionnalité :
|
|
|
A |
O |
|
B |
C |
|
D |
E |
|
|
|
|
relation |
x |
xA |
0 |
1 |
Valeurs choisies
de la variable |
|
||||||
|
« ax » |
y |
yA |
0 |
a |
Valeurs «des « y » obtenues par calcul
|
|
||||||
xA et
yA sont les coordonnées du point A
ces valeurs peuvent se noter verticalement :
![]() A xA ou horizontalement A (xA ,yA)
A xA ou horizontalement A (xA ,yA)
yA
7° ) « a » (dans le produit de facteurs associés à la
fonction linéaire) possède trois appellations , quelles sont -
elles ?
n
Coefficient de proportionnalité (dans le tableau)
n
Coefficient directeur de la droite de la
fonction linéaire.
n
Coefficient directeur de la droit
d’équation y = ax ; dans la
représentation graphique
8° ) Définissez « la
représentation graphique »
précisez ,en
citant les caractéristiques principales ; placer les dans un repère
cartésien.
Les caractéristiques de la représentation
graphique d’une fonction linéaire
sont :
n
c’est une droite (D)
n
cette droite passe par l’origine
« O » d ’ abscisse (0) et d’ordonnée (0) , noté (0 ;0)
n
elle possède un point
caractéristique ; à d’abscisse
valeur « 1 » correspond la
valeur de « a » ;
noté P :(1 ; a)
« a»
s’appelle coefficient directeur de la
droite , c’est un nombre relatif :
Remarques :
si « a »
est « positif » ,dans
la représentation graphique la droite monte de la gauche vers la droite ,on
dira que la fonction est « croissante ».
si « a »
est « négatif » ,dans
la représentation graphique la droite descend du haut gauche du repère vers le bas
droite ,on dira que la fonction est « décroissante ».

![]()
y
![]() 2
2
|
|
![]() 1
1
![]()
![]() +
+![]()
![]()
x
1 2 3
9° ) Comment reconnaît - on une fonction dite « linéaire » ?
son équation de la forme : y =ax
son tableau de proportionnalité
sa représentation graphique ( droite qui passe par O )
Soit les
fonctions :
|
y1 =
2x |
y2 = -
2x |
y3
= - |
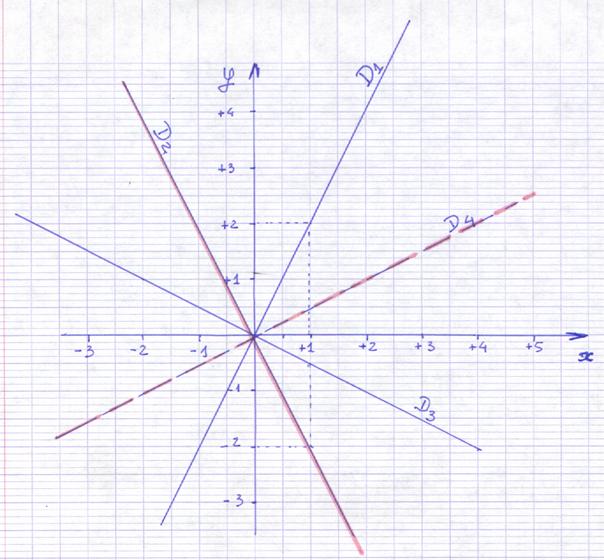
1°) Dans un repère cartésien orthonormé ; Faire
la représentation graphique de chaque fonction .
|
A l' équation
y1 = 2x |
On associe la droite D1 (lire :droite indice 1) |
|
A l' équation
y2 = - 2x |
On associe la droite D2 (lire :droite indice 2) |
|
A l' équation
y3 = - |
On associe la droite D3 (lire :droite indice 3) |
2°) En étudiant le graphique
, donner les coordonnées du point d’intersection des deux droites D1
et D2;
le point
d’intersection est O (0 ; 0 )
3°) tracer D3
Ensuite :
avec un rapporteur donner la valeur de l’angle faite entre les droites D1
et D3 .
Angle = 90°
Quel
commentaire pouvez-vous avoir sur la position des droites l’une par rapport à
l’autre ?
Les deux droites sont perpendiculaires entre elles
.
4° ) Faite le
calcul du produit a1 par a3 .
a1 =
2 ; a3 =
-![]() ; le produit =
; le produit = ![]() = -1
= -1
5°) tracer la droite d'équation y4 = ![]()
a) mesurer l’angle
fait par D2 et D4 (angle = 90 °
)
b) faire le
produit a2 a4 = -2 ![]() = -1
= -1
6°)Comparer les résultats de la question 4° et 5° ; quelle conclusion peut - on en tirer
? lorsque deux
droites sont perpendiculaires le produit de leurs coefficients est égal à -1