Problèmes du premier degré
Ces problèmes sont des prétextes pour faire des mathématiques. Ne vous attendez pas à ce que les situations soient très réalistes...

Un lecteur de cassette et ses écouteurs coûtent 37,5 €. Le lecteur de cassettes coûte 0,50 € de plus que l’écouteur. Quel est le prix du lecteur ? Quel est le prix de l’écouteur ?
Soit p le prix de l'écouteur.
le lecteur de cassettes coûte p + 0,5.
le lecteur et les écouteurs coûtent ensemble p + ( p +0,5 ) = 2p+0,5
donc 2p+0,5 = 37,5
donc 2p = 37
donc p = 18,5.

Le lecteur coûte 19 € et les écouteurs 18,5 € ( penser à vérifier)

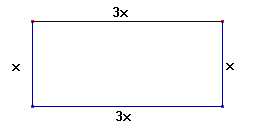
Trouver les dimensions d’un rectangle sachant que la longueur est le triple de la largeur et que le périmètre est 168 m.
Soit x la largeur du rectangle.
la longueur du rectangle est 3x.

Le périmètre est 3x+x+3x+x = 8x
donc 8x = 168, donc x = 21 et 3x = 63

La longueur du rectangle est 63 m et sa largeur 21 m. ( penser à vérifier)

Trouver trois nombres entiers consécutifs dont la somme est 2004.
Soir n le premier nombre. Le deuxième est n+1 et le troisième n+2 .
La somme des trois nombres est n+(n+1)+(n+2) = 3n+3. Elle est égale à 2004.
Donc 3n+3 = 2004 donc 3n = 2001 et n = 667
les trois nombres sont 667,668 et 669. ( penser à vérifier)

Trouver trois nombres entiers consécutifs dont la somme est 2005.
Il n'y a pas de solution car 2005 n'est pas un multiple de 3.

Trois émissions se partagent les 180 minutes d’une cassette de la façon suivante : la première émission dure 13 minutes de moins que la seconde, qui dure elle même 23 minutes de plus que la troisième. Trouver la durée de chaque émission.
Soit d la durée de l'émission la plus courte ( la troisième)
La deuxième émission dure d+23 et la première d+23-13.
La durée totale est d+(d+23)+(d+23-13)=3d+33.
Donc 3d+33 = 180
3d = 147 donc d = 49.

La troisième émission dure 49 min, la deuxième 72 min et la première 59 min. ( penser à vérifier)

Dans une entreprise comprenant 11 ouvriers, 2 contremaîtres et le patron, le total des salaires mensuels atteint 19000 €. Tous les ouvriers ont le même salaire, un contremaître gagne 400 € de plus qu’un ouvrier, et le patron gagne 1000 € de plus qu’un contremaître. Calculer le salaire mensuel d’un ouvrier.
Soit s le salaire d'un ouvrier. Le salaire du contremaître est s+400 et le salaire du patron est (s+400)+1000.
Le total des salaires mensuels exprimé en fonction du salaire d'un ouvrier est :
11s+2(s+400)+s+1400=11s+2s+800+s+1400
                                       =14s+ 2200
Donc 14s+ 2200=19000, donc 14s = 16800, donc s = 1200.
Dans cette entreprise, un ouvrier gagne 1200 €, un contremaître 1600 € et le patron 2600 €. ( penser à vérifier)

Est il possible que dans une classe où tout le monde travaille, que le tiers des élèves écrivent, les quatre septièmes calculent et 2 élèves dessinent ?

Soit n le nombre d'élèves de cette classe.
le tiers des élèves : n
les quatre septièmes des élèves :n
tous les élèves : n+n+3 = n

Il y a 21 élèves dans cette classe : 7 écrivent, 12 calculent et 2 dessinent.

Un père a 27 ans de plus que son fils. Dans 6 ans, son âge sera le double de celui du fils. Quel est l’âge du fils ? du père ?
on exprime les âges en fonction du l'âge actuel du fils, a

	fils	père
âge actuel	a	a+27
âge dans 6 ans	a+6	(a+27)+6=a+33

Dans 6 ans, l'âge du père sera le double de celui du fils, donc :

Le fils a 21 ans et son père 48 ans. ( penser à vérifier)

Trouver la valeur de x pour que le périmètre du triangle équilatéral soit le même que celui du rectangle, sachant que le côté du triangle mesure 7 et la largeur du rectangle est x.
Le périmètre du triangle est 21.
Le périmètre du rectangle est 14+2x
Les deux périmètres sont égaux, donc 14+2x=21
2x =21-14
2x=7
x=3,5
( on aurait pu dire que la longueur du côté du triangle est égale à deux fois la largeur du rectangle!)

À ce jour, l'âge du capitaine est le double de celui de Fred. Dans 5 ans, ils auront à eux deux 70 ans. Quel est l'âge du capitaine ?
a ) Soit x l’âge de Fred. Exprimer en fonction de x :

l’âge actuel du capitaine : 2x

l’âge du capitaine dans 5 ans : 2x + 5

l’âge de Fred dans 5 ans. x + 5

b ) Écrire une équation permettant de résoudre ce problème.
2x + 5 + x + 5 = 70
3x + 10 = 70
3x = 60
x = 20
Fred a 20 ans. Le capitaine a 40 ans. ( penser à vérifier)

Un troupeau est composé de chameaux et de dromadaires. On compte 180 têtes et 304 bosses. Sachant qu’un dromadaire a une bosse et un chameau 2, combien y a-t-il d’animaux de chaque espèce ?
Soit c le nombre de chameaux.
Il y a 180 animaux en tout , donc il y a (180 - c) dromadaires.
J'exprime le nombre de bosses en fonction du nombre de chameaux:
(180 -c) + 2c
Donc (180 -c) + 2c = 304
180 +c = 304
c = 304 - 180
c =124
IL y a 124 chameaux et 56 dromadaires. ( penser à vérifier)

Dans un triangle rectangle, un angle aigu est le triple de l’autre angle aigu. Déterminer la mesure en degrés, du plus petit angle.
Soit a la mesure du plus petit des deux angles aigus. L'autre mesure 3a.
Les deux angles aigus d'un triangle rectangle sont complémentaires. Donc a + 3a = 90
4a = 90 donc a = 22,5
Le petit angle mesure 22,5°.

La somme de quatre nombres pairs consécutifs est 196. Quels sont ces quatre nombres ?
Un nombre pair est un multiple de 2. Soit 2n le plus petit de ces nombres. Le suivant est 2n+2, le suivant 2n+4 et le dernier 2n+6
La somme de ces nombres, exprimée en fonction du plus petit, est donc : 2n+(2n+2)+(2n+4)+(2n+6) = 8n+12
8n+12=196
8n = 184
2n = 46.
Les quatre nombres sont: 46,48,50 et 52. ( penser à vérifier)

RECT est un rectangle. RE = 14, EC = 8.
Comment choisir x pour que l’aire du parallélogramme soit égale à  l’aire restante ?
On calcule l'aire du parallélogramme en enlevant l'aire des deux triangles à l'aire du rectangle.
le deuxième côté du triangle mesure 14-x
Aire d'un triangle: (14-x) 8:2
Aire des deux triangles( aire restante ): (14-x) 8
Aire du rectangle : 112
Aire du parallélogramme : 112 - 8(14-x)
Donc 8(14-x) = 112 - 8(14-x)
16 ( 14-x)=112
en divisant les deux membres par 16, on obtient 14-x = 7 , donc x =7. Ce que l'on pouvait voir dès le départ. Mais on prouve ainsi que c'est la seule solution...

A la cafétéria, cinq élèves ont commandé un soda, un jus d’orange et trois chocolats.
Les cinq  consommations reviennent à 4,30 €.
Un soda coûte 0,30 € de plus qu’un chocolat.
Un jus d’orange coûte 0,50 € de plus qu’un chocolat.
Calculer le prix d’un chocolat, puis d’un soda et d’un jus d’orange.
Soit p le prix de la consommation la moins chère, donc du chocolat.
En fonction de p, le prix d'un soda est p+ 0,3 et le prix du jus d'orange p+0,5.
Le prix total est alors (p+ 0,3)+(p+0,5)+3p = 5p+0,8
Donc 5p+0,8 = 4,3
5p = 3,5
p=0,7
Un chocolat coûte 70 centimes, un soda 1 € et un jus d'orange 1,20 €

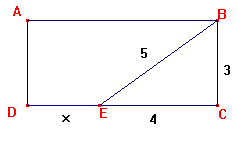
ABCD est un rectangle.
Soit E un point de [ CD ] tel que DE = x et EC = 4.
De plus BC = 3 et  BE = 5.
Calculer x pour que le périmètre du trapèze ABED soit le double de celui du triangle BCE.
J'exprime en fonction de x le périmètre de ABED:
x+3+(x+4)+5 = 2x+12
le périmètre de BEC est 12
Donc 2x + 12 = 24
2x = 12 donc x = 6
Pour que le périmètre du trapèze ABED soit le double de celui du triangle BCE il faut que x soit égal à 6.

Voici la règle d'un jeu :   
Quand on gagne, on reçoit 3 euros. Quand on perd, on donne 1,2 euros.
Amélie a joué 25 fois à ce jeu et elle a perdu 0,6 euros au total.
Combien de fois a-t-elle gagné ?

Soit x le nombre de fois où Amélie a gagné. En tout, elle a gagné 3x euros.

Elle a joué 25 fois et gagné x fois, donc elle a perdu 25 - x fois.
Elle a perdu en tout 1,2(25 - x) euros.

En tout, elle a 3x - 1,2(25 - x) euros, et cela lui donne une perte de 0,6 euros, donc -0,6 euros.
Il faut donc résoudre l'équation :

3x - 1,2(25 - x) = -0,6
3x - 30 + 1,2x = - 0,6
4,2x =-0,6 + 30
4,2x = 29,4

donc x = 29,4 : 4,2

x = 7.
Amélie a gagné 7 fois ( et perdu 18 fois ! )

Merci au professeur de Guillaume pour ce joli problème.