Leçon	Titre
N°22	LES RELATIONS TRIGONOMETRIQUES dans le triangle rectangle .

Corrigé EVALUATION formative (niveau V) :

1 °) Utiliser la calculatrice pour trouver le sinus , cosinus et tangente des angles : 7° ; 30° ; 84°.

Angle :	Sinus	Cosinus	Tangente
7°	0,12186934340514	0,99254615164132	0,12278456090290
30°	0,5	0,86602540378443	0,57735026918962
84°	0,99452189536827	0,10452846326765	9,51436445422258

( en général on arrondit au 0,001 près )

2°) Utiliser la calculatrice pour trouver la valeur de : (donner la valeur décimale affichée , puis la valeur décimale arrondie à 0 ,001 prés.

a) l’angle C dont le sinus est 0,876 5 ,

b) l’angle A dont le cosinus est 0,423 6

c) l’angle B dont la tangente est 1,973 2

Solution :

- sinus 0,876 5 = 61,22 30002674563870029460466444187° » 61,22° ; l’angle C » 61,22° 

- cosinus 0,423 6 = 64,9379198941684120820136530194404 » 64,94 ° ; l’angle A » 64,94 ° 

- tangente 1,9732 =63,1245186381872560194775281181102 » 63,12° ; l’angle B » 63,12 °

3°) Calcul de la longueur d’un côté connaissant un angle et la longueur d’un autre côté .

Soit un triangle CBA rectangle en B .

On donne l’angle A = 42° et [B A] = 20 cm.

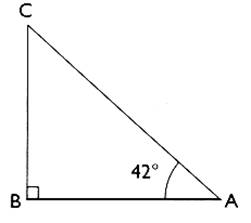
Question : on demande de calculer la longueur du côté [ B C] .

Procédure :	Solution :
1°)inventaire des données : [BA] est le côté adjacent à l’angle A. On obtient ,avec la calculatrice, la valeur décimale de : Sin 42° : 0,669 1 Cos 42° : 0,743 1 Tan 42° : 0,9004	[BA ] = 20 cm et = 42 °
2°) Etablissement des formules : ( à partir des 3 définitions)	Sin = ;cos = ; tan =
Analyse :La relation trigonométrique « tan » est la seule formule utilisable avec les données . Il faut convertir tan 42° en valeur décimale avec la calculatrice .	tan = tan 42° = 0,900404044297839945120477203885372
3°) calcul de CB à partir de l’égalité : tan =  ; On remplace les lettres par les valeurs connues .	0,9004 =
4°) transformation ( produit en croix) =	20 0,9004 = 1 CB CB = 18,00 cm

4°)Dans le triangle rectangle ci - dessous :

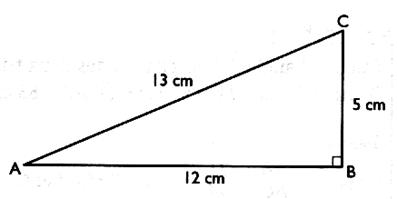
Question : Etablir les rapports trigonométriques et calculer les valeurs de :

=  ; =  ; = et puis

= , = ; = .

Au regard des résultats trouvés ; quelles conclusions ou remarques pouvez vous formuler ?

Solution :

=	=	=
» 0,384 6	» 0,923 1	» 0 , 416 7
» 0,384 6	» 0,923 1	» 0 , 416 7

» 0,923 1	» 0,384 6	= 2,4
» 0,923 1	» 0,384 6	= 2,4

On remarque que  :

- » 0,384 6 et » 0,384 6 , donc …=…..

- » 0,923 1 et » 0,923 1 ; donc ……=….

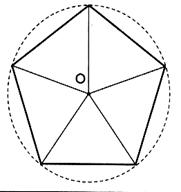
5 °) On considère un pentagone régulier inscrit dans un cercle de rayon 6 cm .

a) Quelle est la nature de chacun de ces cinq triangles dont le sommet est le centre "O" du cercle . le triangle est un triangle isocèle .( 360 ° / 5 = 72° )

b) Donner une mesure de chacun de leurs angles . ( rappel :la somme des angles d'un triangle est de 180 ° ) . si l’angle au sommet 72° ; la somme des deux autres angles = 180 - 72° = 108 ° ; un angle de base = 108° :2 = 54°

c) Calculer l'aire de ce pentagone . ( pour calculer "h" , la hauteur d’un triangle , utiliser la trigonométrie) .

Aire d’un triangle : il faut savoir calculer la hauteur « h » , distance qui va du centre à la base ? ( voir la trigonométrie )

Hypoténuse = 6 cm ; hauteur : sinus 54° = 0,809 = h / 6 ; donc h = 6 fois 0,809 = 4,85 cm ; base : cos 54° = 0,588 = b / 6 = 6 fois 0,588 = 3,53)

Un demi triangle : ( 4,85 fois 3,53 ) / 2 = 17,12 cm² ; il y a 10 demi - triangles équilatéral ; l’aire du pentagone = 17,12 fois 10 = 171,2 cm²