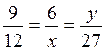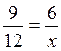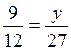|
Titre |
|
|
N°21 |
CORRIGE :PROPRIETE de
THALES. |
1°)
Enoncer la propriété de Thalès pour un triangle .
|
En
utilisant les caractéristiques de la
figure ci - contre . |
|
|
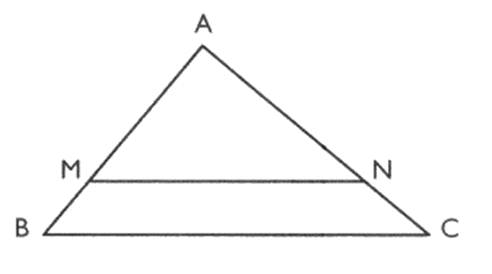
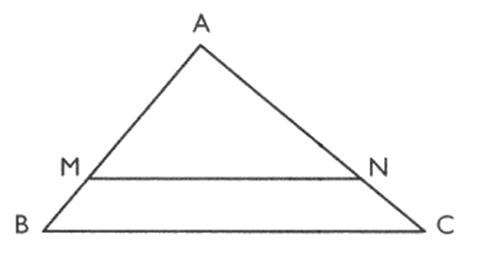
Si dans un triangle A BC , une
parallèle à un segment [ BC] coupe un segment [ AB]
en M et un segment [ AC ] en
un point N alors on a |
|
2°)
Enoncer la propriété de Thalès relatif
à deux droites sécantes coupées par 3 parallèles.
( vous aider d'un dessin)
EVALUATION:
Exercices traités dans le cours :
1°)
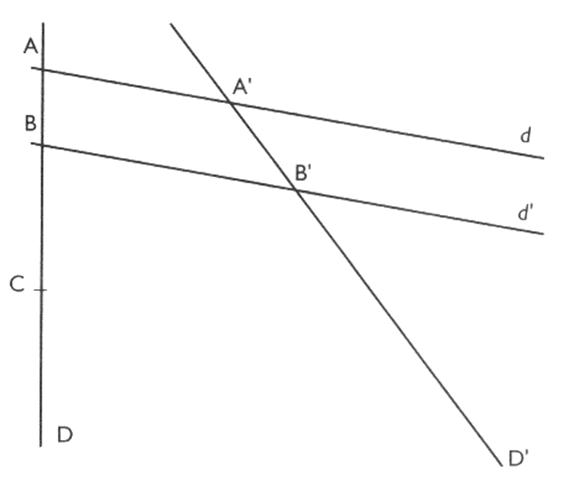
Sur la figure , on a tracé D et D' quelconques coupées par deux droites parallèles "d" et "d'
" .
|
"d" coupe D en A et D' en A' . et "d' " coupe D' en B et B' . |
|
|
Tracer une parallèle à d et d' passant par C
et coupant D' en C' .
Relever les mesures et vérifier que ![]()
Environ : 1,5
2°) Soit la figure ci - dessous
.
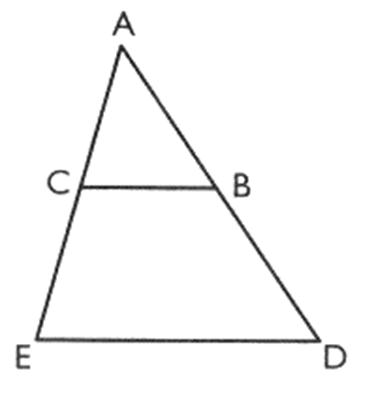
On donne : le segment BC parallèle au
segment DE , le segment AB =
![]() donc
donc ![]() ; AD = (
17 fois 20 ) divisé par 12 ; AD = 18 ,33cm
; AD = (
17 fois 20 ) divisé par 12 ; AD = 18 ,33cm
3°) On donne la figure ci-dessous :
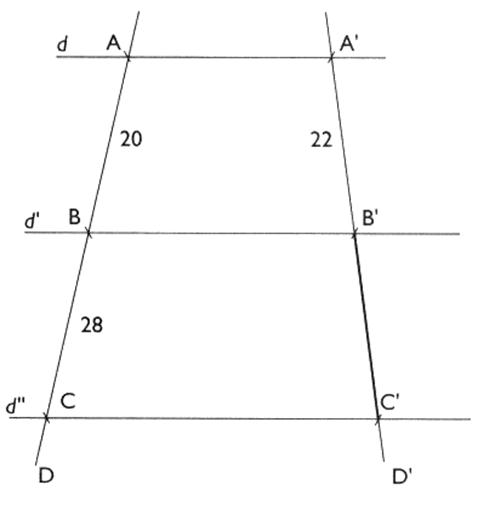
AB =
D'après
la propriété de Thalès, on peut écrire :
![]()
Les
données sont : AB = 20 ; A'B' = 22 ; BC = 28 ; B' C' = ? ;
Et AC = (20 +28) = 48 ; A'C' =
(22 + B’C’) ;
On
remplace : ![]()
On cherche A'B' , on retient deux rapports dont on connaît 3 valeurs sur 4 .
![]() ; 20 fois x
= 22 fois 28 ; 20 x =
616 ; x = 616 : 20 ; x = 30,8
; 20 fois x
= 22 fois 28 ; 20 x =
616 ; x = 616 : 20 ; x = 30,8
donc B'C’ =
Exercices
non traités dans le cours :
|
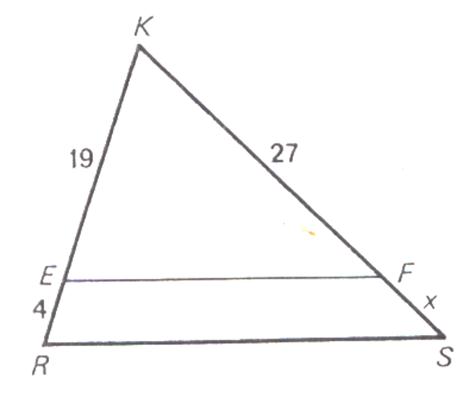
N°1 : Calculer « x »
x
= (27´4) /19 x
= 5,68 |
|
|
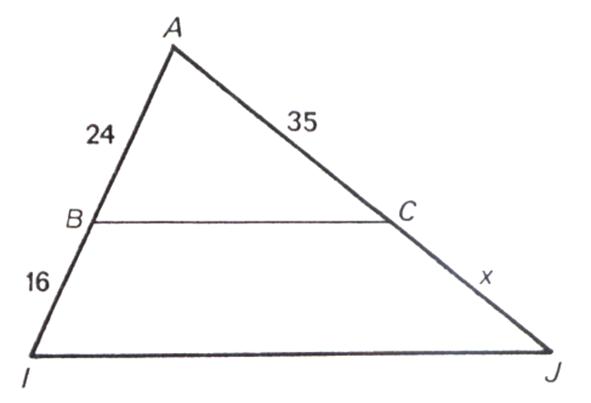
N°2 : Calculer « x »
x
= (35´16) /24 x
= 23,33 |
|
|
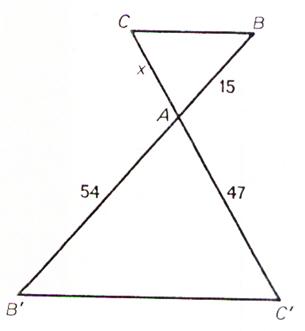
N°3 : Calculer « x » :
x = ( 47 ´ 15 ) / 54 x =
13 ,05 |
|
|
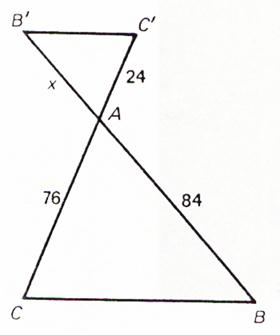
N°4 : Calculer « x » :
x = ( 24 ´ 84 ) / 76 x =
26,53 |
|
|
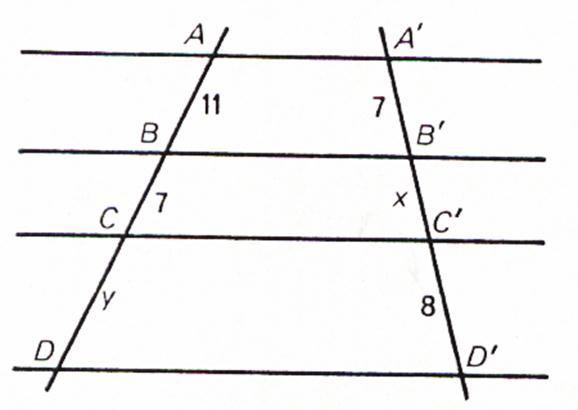
N°5 : Calculer « x » et « y »
on en déduit 2 rapports égaux :
y
= ( 8 fois 11) divisé par 7 y
= 12,57
x = (7 fois 7) divisé par 11 x
= 4,45 |
|
|
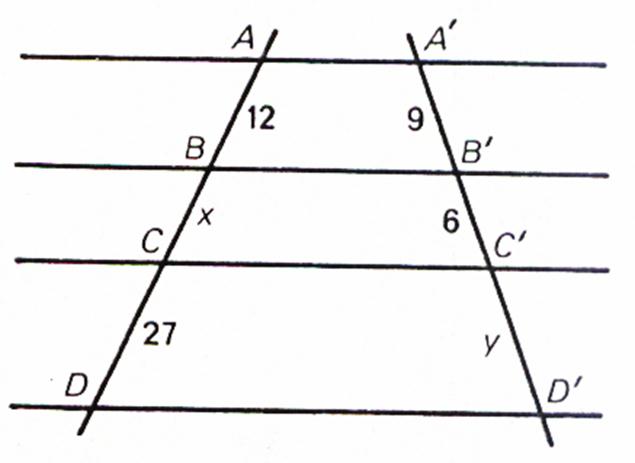
N°6 : Calculer « x » et « y »
9/12 = 6/x = y / 27 donc x = 8 ; et y = 20,25 On en déduit 2 rapports égaux dont on connaît 3 valeurs sur 4 : x = (6 fois 12) divisé par 9 x =
72 :8 = 9
y = ( 9 fois
27 ) divisé par 12 y
= 20,25 |
|