|
Titre |
|
|
N°20 |
CORRIGE : TRAVAUX d ’ AUTO - FORMATION sur PYTHAGORE Le
théorème ; la Propriété de PYTHAGORE et sa réciproque. |
1°)
Enoncer le théorème de Pythagore.
Dans un triangle rectangle , la somme
des carrés des longueurs des côtés formant l'angle droit est égale au carré de la longueur de l'hypoténuse
.
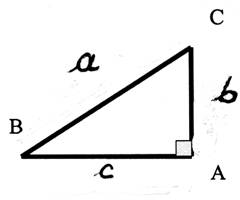
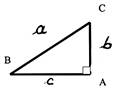
2°) Soit
le triangle BCA :
|
a) Etablir la relation permettant de calculer
: BC ² = CA ²
+ BA ² |
|
3°)
Enoncer la réciproque de Pythagore.
Si dans un triangle , le carré de la longueur d'un côté
est égal à la somme des carrés
des autres longueurs des deux autres côtés
, alors le triangle est rectangle .
4°) Citer 3 possibilités permettant d ’
identifier un triangle rectangle .
Pour
identifier un triangle rectangle , on peut :
-
vérifier que ses dimensions
satisfont la réciproque de la
propriété de Pythagore ;
-
vérifier qu'il est inscrit dans un demi - cercle dont le
diamètre est l'hypoténuse du triangle .
-
vérifier qu'un de ses
angles est droit à l'aide d'une équerre
ou un rapporteur .
4°) Compléter le tableau
|
« Le triangle est
rectangle ! ! ! !» |
||||||
|
|
||||||
|
|
a |
750 mm |
37 cm |
53 cm |
0,65 m |
295 mm |
|
b |
450 mm |
35 cm |
45 cm |
0,56 m |
2,36 dm |
|
|
c |
600 mm |
12 cm |
280 mm |
0,33 m |
72,31 mm |
|
I
) 450² + 600² = 202500
+ 360000 = 562500 ; racine carrée
de 562500 = 750 mm
II) 37² -35² =
c² ; c² = 1369 -
1225 = 144 ; c = 12 cm
III) 28² +
45 ² = 784 + 2025 = a² ; a = 53 cm
IV) 0,65 ² - 0,33 ² = b² ;
0,4225 - 0,1089 = 0,3136 ; b = 0,56 m
V) 295² - 236 ² = 87025 - 81796 ; c = (environ
à 0,01 prés) 72,31 mm
Série II
|
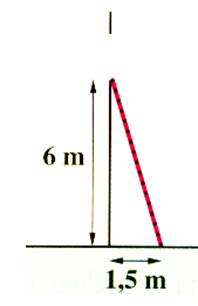
N°2 : Quelle longueur doit mesurer une échelle pour atteindre une
fenêtre située à 6 m. Si on lui donne 1,5 mètres de pied ? D’après Pythagore : (Longueur de l’échelle ) ² = 6 ²
+ 1,5 ² (Longueur de l’échelle ) ² = 36 + 2,25
(Longueur de l’échelle ) ² = 38,25
Racine carrée de 38 ,25 = 6,18 4658438 L’échelle devra mesurer plus de 6,18 m |
|
|
N° 3 : Calculer la diagonale DB
du cube au dixième près. DB²= DA< ² + AB² DB² = 4²+ 4² DB² = 32 DB = DB = 5,656854………. DB = 5,7 à 0,1 prés N° 4 : Calculer la diagonale DF
du cube au dixième près. DF² = DA²
+ AF² Puisque c’est un cube : DB = AF Donc DB² = AF² = 32 Donc : DF² = 4² + 32
DF² = 16 + 32 DF² = 48 DF = DF = 6 , 9282 DF = 6,9 à 0,1 prés . |
|