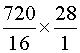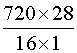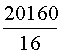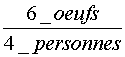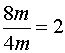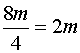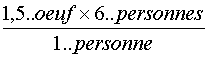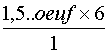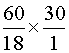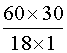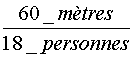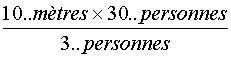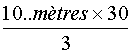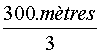CORRIGE
8 ° )
Enoncer la procédure permettant d’effectuer « la règle de trois ».
la "règle de
trois" est une transformation du "produit en croix" ,pour régler la recherche d'une quatrième grandeur (appelée "quatrième
proportionnelle" ).
Rechercher la quatrième proportionnelle :
On
dirait aussi : Transformer , par
le produit en croix , les fractions équivalentes :
|
|
|
|
|
|
|
|
|
et
encore :
a) ![]() = 5
b)
= 5
b) ![]() = 7 ;
= 7 ;
Transformer
, par le produit en croix , les fractions équivalentes :
|
|
5x =36 |
|
35=3x |
|
7x =36 |
|
35=12x |
|
|
X= 7,2 |
|
X= 35/3 |
|
X=36/7 |
|
X=35/12 |
a) ![]() = 5
b)
= 5
b) ![]() = 7 ;
= 7 ;
|
Enoncé 1:
Sachant que 16 m de tissu ont été
payés 720 F ,trouvez le prix de 28m. |
|
Résolution
: Le prix étant proportionnel à la longueur , le prix cherché est :
au lieu d'utiliser les fractions , on peut employer la
méthode de "réduction à l'unité". Le prix du mètre de tissu
est de Le prix de 28 m est de 45 |
|
Enoncé:
Sachant que pour faire un gâteau de 4
personnes six œufs ,combien faut-il d'œufs pour faire un gâteau de 6
personnes ? |
|
Le nombre d'œufs étant proportionnel au nombres de
personnes , le prix nombre d'œufs
cherché est : Explication du calcul:
Au lieu
d'utiliser les fractions , on peut employer la méthode de "réduction à
l'unité". Le nombre d'œufs par personne est de Le nombre d'œufs pour 6 personnes est
de 1,5 A propos des unitésL qui s' annulent par la division: les unités de même "famille" s ' 'annulent dans la division: exemple:
soit : |
|
Enoncé: Un
entrepreneur fait construire d '
habitude une maison en 60 jours avec 15 ouvriers .six personnes tombent malades, déterminer
la durée des travaux . Il n ' y
a pas de proportionnalité : le travail de l'ensemble des personnes ne peut se
réduire au travail d'un seul individu
. |
|
Résolution
: La durée des travaux étant proportionnel aux nombres de
personnes , la durée cherchée est : Le nombre de jours
est constant : 60 Il y a 15 - 6 = 9
ouvriers pour effectuer les 900 jours
de travail Conclusion: 900 :
9 =100 ; il faudra 100 jours pour construire la
maison. |
|
Enoncé
N° 4: 18 ouvriers ont
fait , dans des conditions déterminées
, 60 mètres d'ouvrage. Combien 30 ouvriers feraient-ils de mètres du même
ouvrage, toutes les autres conditions restant les mêmes ? |
|
Les deux
grandeurs sont directement proportionnelles . Le
nombre de mètres construit étant
proportionnel au nombres de personnes
, le nombre de mètres
cherchés est : Explication du calcul:
Au lieu
d'utiliser les fractions , on peut employer la méthode de "réduction à
l'unité". Le nombre de mètre par
personne est de
Le nombre de mètres pour 30
personnes est de 10/3 A propos des unitésL qui s' annulent par la division: les unités de même "famille" s ' 'annulent dans la division: exemple:
soit : |
|
|
|
|
X = 5 fois 13 X= 65 |
13 fois 1 = 7 fois x 13 =7 x 13/7 = x ou x = 13/7 |