|
Titre |
|
|
N°19 |
CORRIGE TRAVAUX d ’ AUTO - FORMATION sur GEOMETRIE
dans L ’ ESPACE et AIRES et " VOLUME de solides usuels " |
1°) Compléter le tableau
suivant:
|
Symbole |
Correspondance en m3 en
valeur décimale et sous forme de puissance de 10 |
|
|
Kilomètre cube |
km3
( = 1000m)3 |
1
km3 =1 000 000 000 m3 = 1 ´
10 9 m3 |
|
Hectomètre cube |
h m3 ( = 100m)3 |
1 h m3 = 1 000 000 m3
= 1 ´
10 6 m3 |
|
Décamètre cube |
da m3 ( = 10m)3 |
1da m3 = 1 000 m3 = 1 ´ 10 3 m3 |
|
Mètre
cube |
m3 ( = 1m)3 |
1 m3 = 1´
10 0 m3 |
|
Décimètre cube |
d m3 ( = 0,1m)3 |
1 d m3 =
0 , 001 m3 = 1 ´ 10 -3 m3 |
|
Centimètre cube |
c m3 ( = 0,01m)3 |
1 c m3 =
0, 000 001 m3 = 1 ´ 10 -6 m3 |
|
Millimètre cube |
m m3 ( = 0,001m)3 |
1 m m3 = 0 , 000 000 001m3 =
1 ´ 10-9 m3 |
2°) Compléter la phrase suivantes :
Les unités principales de mesure de volumes et de
capacité sont : Le mètre cube et le litre .
Un litre a un volume
égal à un
décimètre cube .
Il faut savoir que 1 décimètre cube ( dm3)
contient un volume équivalent à 1 litre d’eau pur à 4°
Centigrade .
· mesures équivalentes :
1dm3 = 1 l
; Un litre = 100 cl ; 100 cl = 1 dm3
= 1000 cm3 donc 1cl
= 10 cm3
et 1m3 = 1000 dm3 = 1 000
litres ; 1 cm3 = 1000
mm3
3°) tracer le tableau de
conversion des unités de volumes ( et capacité ) .
|
km3 |
hm3 |
dam3 |
m3 |
dm3 |
cm3 |
mm3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kl |
hl |
dal |
l |
dl |
cl |
ml |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4°) Donner la procédure permettant de transformer l ' unité de volume
en multiples ou sous multiples à partir d'une grandeur donnée.
Pour remplir le tableau en vue de faire une
conversion il faut respecter la procédure
suivante:
1°) placer la virgule du nombre donné sur le trait
vertical "droit" de l'unité donnée.( da m3 , )
2°) placer les chiffres du nombre dans en
respectant l '
ordre donné :
3°) il faut déplacer le virgule ; la mettre sur le trait vertical
"droit" de l' unité "demandée " (d m3 , ) compléter de
"zéros" éventuellement !
4° ) il suffit de
reporter le résultat , (lu sur le
tableau )
5°) Pour effectuer la perspective cavalière d'un cube ,quelles sont
les informations que l'on doit posséder ?
Pour effectuer la perspective cavalière du
cube il faut connaître comme dimensions : la longueur de son côté , le coefficient
"k" , et l'angle alpha .
6°) Pour effectuer la perspective cavalière d'un
parallélépipède rectangle ,quelles sont les informations que l'on doit posséder ?
Pour effectuer la perspective cavalière du
parallélépipède rectangle il faut
connaître comme dimensions : la longueur , la hauteur
, la largeur , ( ou profondeur) , le coefficient "k" , et
l'angle alpha .
7°) Donner la procédure
à appliquer pour effectuer la
perspective d’un parallélépipède rectangle.
Procédure : tracer la face en vraie grandeur ,
puis les fuyantes inclinées de alpha par rapport à l' horizontal . Calculer la
longueur des fuyantes , limiter la longueur des
fuyantes , tracer les verticales .
8°) Cube : Si
la longueur de l'arête est
notée "a" . donner
les formules permettant de calculer :
l' Aire
latérale = 4 a² ; l ' Aire totale = 6 a² ; le Volume du cube = a3 .
9°) Parallélépipède rectangle .
Donner
la formule permettant de calculer
Aire latérale ;
Aire totale ;
Volume ;
Compléter la phrase :
pour les calculs les dimensions doivent
être exprimées dans "………………… "
de longueur .
Solution
:
1°) on convertit dans la même unité ( cm) les dimensions :
.
2°) Aire latérale ( somme
des aires des côtés latéraux ) :
A l = 2 h
( L + l )
=
3°) Aire totale
( somme des aires des côtés latéraux et des
bases ) :
A t = 2 h ( L + l )
+ 2 L l =
4°) Volume
du parallélépipède rectangle
:
V = L l h =
10° ) Cylindre :
La hauteur étant notée : "h" et le rayon :
"R"
L'aire latérale : A l
= 2p
R h .
L'aire de la base ( et de
la face supérieure ) : A b = 2p
R ²
L'aire totale
( l'aire latérale + l'aire des deux disques) =
2p
R h + 2 (2p R ² )
Volume
: V = aire d'une base ![]() hauteur ;
V = 2p
R ² h
hauteur ;
V = 2p
R ² h
TRAVAUX N° d
’ AUTO - FORMATION :
EVALUATION
1°)
convertir :
32,24 dam 3
= 32 240
000 dm3 = 32 240 m3
= 0,032 24 hm3 ;
= 32 240 000 000
000 mm3
= 32 240 000 000
cm3
2°)Placer 1 765 , 798
m3 ; 5,3 m3 ; 78 507 dm3 ; 2854 cm3 ; 5 832 mm3 dans le tableau ci - dessous :
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
|
dm3 |
|
cm3 |
|
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
solutions :
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
, , |
dm3 |
, |
cm3 |
, |
mm3 |
, |
||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
7 |
6 |
5 |
7 |
9 |
8 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
7 |
8 |
5 |
0 |
7 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
8 |
5 |
4 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
8 |
3 |
2 |
|||||||
Suite :En utilisant
le tableau ci dessous convertir :
1 765 , 798
m3 en ………………………………dm3
5,3 m3 = ………………………..dm3
78 507 dm3 = ……………………m 3
2854 cm3 = ……………………m3
5 832 mm3 = …………………….cm3
Solutions
: on
reprend le tableau rempli dans l’activité 1
On fait dans l’ordre : On
complète de zéro ; on retire la virgule ; la déplacer dans la colonne de droite de l'unité demandée.
|
km3 |
|
hm3 |
|
dam3 |
|
m3 |
, |
dm3 |
,, |
cm3 |
, |
mm3 |
|
||||||||||||||
|
|
|
|
|
|
|
0 |
0 |
1 |
7 |
6 |
5 |
7 |
9 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
5 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
7 |
8 |
5 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
2 |
8 |
5 |
4 |
0 |
0 |
0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
8 |
3 |
2 |
|||||||
1 765 , 798 m3 = 1 765
798 dm3 ;
5,3 m3
= 53 000 dm3
78 507 dm3
= 78, 507 m 3
2854 cm3 = 0, 002 854 m3
5 832 mm3 = 5
, 832 cm3
2°)Compléter le tableau de
conversion:
|
|
1 m3 |
1 dm3 |
1 cm3 |
1 mm3 |
|
1 m3 |
1 |
1 000 |
1 000 000 |
1 000 000 000 |
|
1 dm3 |
0,001 |
1 |
1000 |
1 000 000 |
|
1 cm3 |
0,000 001 |
0,001 |
1 |
1 000 |
|
1 mm3 |
0,000 000 001 |
0,000 001 |
0,001 |
1 |
3°) Convertir
successivement : (
il suffit pour trouver les
conversions successives de déplacer la virgule et de relever le résultat
).
1 765 , 798
m3 en ……1 765 79 8 ……dm3
1 765 ,
798 m3 en …1 , 765 798
…dam3
5,3 m3 = ………5300………..dm3 = ……5 300 000……cm3
;
78 507 dm3 = ……78,507…m 3
= ……78 507 000…cm3;
2854 cm3 = 0,002 854
m3 =2,854dm3
= 2 854 000 mm3.;
5 832 mm3 = 5
, 832 cm3 = 0,005 832 dm3
4°)Convertir dans l '
unité demandée:
|
|
Convertir en : |
Convertir en : |
validation |
||
|
270 dl |
27 |
l |
2,7 |
dal |
|
|
1,52 l |
1520 |
ml |
0,00152 |
kl |
|
|
212,33 kl |
21233 |
dal |
2123,3 |
hl |
|
|
11,50 l |
1150 |
cl |
0,1150 |
hl |
|
|
270 d m3 |
0,270 |
m3 |
0,000 270 |
dam3 |
|
|
1,52 m3 |
1520 000 000 |
m m3 |
0,000 000 00152 |
k m3 |
|
|
212,33 k m3 |
212330 000 |
dam3 |
212330 |
h m3 |
|
|
11,50 m3 |
11500000 |
c m3 |
0,00001150 |
h m3 |
|
|
125600 m m3 |
125,6 |
c m3 |
0,1256 |
d m3 |
|
|
6,75 d m3 |
6,75 |
l |
67,5 |
dl |
|
|
1419000 cm3 |
1,419 |
m3 |
1419 |
d m3 |
|
|
27900 da m3 |
h m3 |
27 900 000 |
m3 |
|
|
|
22,4 dal |
0,224 |
m3 |
2240 |
d m3 |
|
|
119 cm3 |
119 |
ml |
0,119 |
l |
|
5°) Perspective cavalière :
Dessiner un cube d'arête 5 cm en perspective cavalière avec
l'angle µ = 30°
et k = 0,4.
6°)Le
CUBE :
Description :
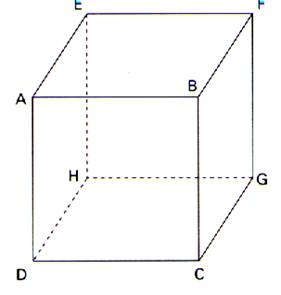
Citer :
-
deux arêtes parallèles : exemples AB //DC
//HG//EF ; ou AD//BC//FG//EH ; ou AE//FB//GC//HD…
-
deux arêtes perpendiculaires : …AB et BC ; AB et FB ………………………..
-
Deux faces parallèles :…exemples : (ABCD) et (EFGH) ; (BFGC) et ( AEHD) ;
(AEFB) et (DHGC)
Deux faces perpendiculaires: …exemples :
(ABCD) et ( AEFB) ou et (BFGC)…et ainsi de suite.
Calculs :
7°) Un cube a une arête de longueur
"a = 30 mm"
Calculer :l' aire latérale ( en mm² et cm² ) , l'aire totale ( cm²)
, le volume du cube ( mm3 puis cm3 ) .
Solution
:
Aire latérale ( 4 faces ) :
A = 4 a² ; A = 4 fois 30 fois 30 = 4 ![]() 30
30 ![]() 30
= 3 600 mm² ; ou
36 cm²
30
= 3 600 mm² ; ou
36 cm²
Aire totale ( 6 faces) :
A = 6
a² ;
A = 6 fois 3 fois 3 = 6 ![]() 3
3 ![]() 3
= 54
cm²
3
= 54
cm²
Volume du cube :
V = a3 ; V = 30![]() 30
30![]() 30
= 27 000 mm3 ou 27
cm3
30
= 27 000 mm3 ou 27
cm3
8°) Le parallélépipède rectangle :
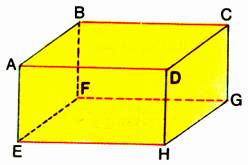
Citer :
-
deux arêtes parallèles : …exemple……EF
//HG…………
-
deux arêtes perpendiculaires : …exemple……AD et
DC…………………..
-
Deux faces parallèles :…exemple……(ABFE) et ( DCGH)
-
Deux faces perpendiculaires: ……exemple : ( ABFE ) et ( FGHE)
.
9°) Représentation graphique du parallélépipède rectangle :
De la même façon que pour le cube , représenter en
perspective cavalière un parallélépipède rectangle de longueur 7 cm ,
de largeur 5 cm et de hauteur 3 cm avec
un angle "alpha" = 45 ° et
"k" = 0 , 6
10°)Calculs
Parallélépipède rectangle .
Un
parallélépipède rectangle a pour
dimensions : L
= 7,5 cm ; l = 50 mm ; h = 0,2 dm .
Calculer l'aire
latérale , l'aire totale ( exprimées en cm² et mm² ) et le volume ( exprimé en mm 3 et cm3 ).
Solution
:
1°) on convertit dans la même unité ( cm) les dimensions :
L = 7,5 cm =
; l = 50 mm = 5 cm ; h = 0,2 dm =
2 cm .
2°) Aire latérale ( somme
des aires des côtés latéraux ) :
A l = 2 h
( L + l )
= 2 ![]() 2
( 7,5 + 5 ) = 50 cm² ; = 5000 mm²
2
( 7,5 + 5 ) = 50 cm² ; = 5000 mm²
3°) Aire totale
( somme des aires des côtés latéraux et des
bases ) :
A t = 2 h ( L + l )
+ 2 L l = 2 ![]() 2
( 7,5 + 5 ) + 2
2
( 7,5 + 5 ) + 2 ![]() 7,5
7,5 ![]() 5 ;
5 ;
= 50 + 75 cm² = 125
cm²
4°) Volume
du parallélépipède rectangle
:
V = L l h = 7,5![]() 5
5 ![]() 2 = 75 cm3
2 = 75 cm3
10°) Calculs sur le
cylindre :
Un cylindre a pour
dimensions : h = 110 mm et R =
52 mm ; prendre pi = 3,14
Calculer L'aire latérale
( en mm² et cm² ) ; L'aire de la base ( en mm²
et cm² ); L'aire totale ( en mm² et cm² ); le volume ( en mm3 et cm3
).
Solution
:
a) L'aire latérale :
A l = 2p
R h . ; A l = 2 ![]() 3,14
3,14
![]() 52
52 ![]() 110
= 35921,6 mm² ou 359 , 216 cm²
110
= 35921,6 mm² ou 359 , 216 cm²
b) L'aire de la base ( et
de la face supérieure ) :
A b
= 2p
R ² ; = 2 ![]() 3,14
3,14
![]() 52
52 ![]() 52 =
16981,12 mm² soit 169 ,8112 cm²
52 =
16981,12 mm² soit 169 ,8112 cm²
c) L'aire totale
( l'aire latérale + l'aire des deux disques) :
A t
= 2p
R h + 2 (2p R ² )
=
35921,6 + 16981,12 =52902,72 mm² ou 529,
0272 cm²
d) Volume : V =
aire d'une base ![]() hauteur ;
hauteur ;
V = 2p
R ² h ; 2 ![]() 3,14
3,14
![]() 52
52 ![]() 52
52 ![]() 110 =
1867923,2 mm3 ou 1867,9232 cm3
110 =
1867923,2 mm3 ou 1867,9232 cm3