|
Leçon |
DEVOIR de remédiation. |
|
N°15 |
PERPENDICULAIRE - DISTANCE -
HAUTEUR et MEDIATRICE d'un
segment et BISSECTRICE d'un angle -
MEDIANE. |
TRAVAUX N° 15 d ‘
AUTO - FORMATION EVALUATIONSérie 1 :
A)
Perpendiculaire et Projetée orthogonale
1°)
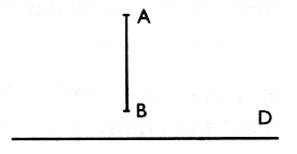
Projection orthogonale d'un segment sur une droite :
a) Reproduire la figure . Construire A' et
B' , projetés orthogonaux de A et B respectivement sur ( D) ,
et tracer [ A ' B' ] : le segment [ A '
B' ] est le projeté orthogonal du segment [A B] .
b) Placer
le point M , milieu de [A B] et
construire M' son projeté orthogonal sur ( D )
. Quelle est la position de M' sur [ A ' B' ]
Tracé 1
|
|
|
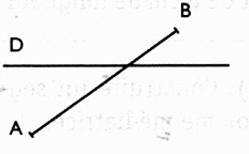
Tracé 2
|
|
|
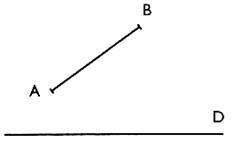
Tracé 3 :
|
|
|
B
) Distance :
1°) tracer
une droite ( D ) et placer un point distant de 5 cm de ( D)
.
2°) sur une
carte au 1 / 100 000 on trouve quatre
villes A ; B ; C et D .
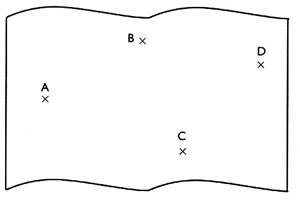
A
l'aide du compas seulement , classer les
distances AB ; BC ; BD ; AC ; AD et CD dans l'ordre décroisant .
C )
Médiatrice :
1°)
Construire à la règle et au compas la
médiatrice d'un segment de droite de
7,5 cm de longueur .
2°)Placer 3
points non alignés A , B et C tels que :
AB = 3 cm ; BC = 4 cm et ![]() = 120° .
= 120° .
Construire
la médiatrice du segment AB puis celle du segment BC ; elles se coupent en un
point " I " .
Tracer le
cercle de centre "I" et de rayon " I A " .
Que
constate - t- on ? Justifier la réponse .
3°) On
donne un point "B" Construire
une droite (d) dont la distance de "B" est de 2,5 cm.
D )
Bissectrice .
Tracer la
bissectrice de l'angle .
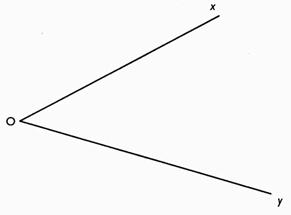
1°) Construire deux droites
parallèles situées à 5 cm l'une de
l'autre .
pour cela :
-
Tracer une droite ( D).
-
Tracer une droite (d) perpendiculaire à ( D) qui coupe ( D)
en "H" . ( utiliser l'équerre)
-
Placer sur (d) le point "M" situé à 5 cm de "H" . (
il y a deux solutions )
-
Tracer la droite ( D') perpendiculaire à ( d ) et passant
par M .
2°) Construire à la règle et au compas
la médiatrice ( D) d'un segment AB de 6
cm de longueur . Soit "F"
le point d'intersection de ( D)
et de [ A B ] .
Placer sur la médiatrice deux points C et D situés de part et d'autre de F tels que F
soit le milieu de [ C D ] . Que
représente la droite ( AB) pour le segment [ CD] . Quelle est la nature du quadrilatère ACBD ?
3°) Placer trois points A , B et C tels que
AB = 5 cm , BC = 6 cm , AC = 7 cm. Construire la médiatrice
du segment [ AC] puis celle du segment
BC . Elles se coupent en O .
Tracer le cercle de centre
"O" et de rayon OA . Les points B et C appartiennent - ils au
cercle ? Justifier la réponse .
Vérifier
que la médiatrice du segment AB passe
par le point I .