|
NOM :
. Prιnom :
|
Mathιmatique Tronc Commun. Fonction linιaire. |
C C F :niveau V Sit.n°6 B |
|
|
Obj. |
Capa. |
||
SUJET 1
|
TC2 |
E |
T |
C |
|
1°) On donne
les tableaux de variation des fonctions f1 et f2 |
|
|
|
|
|
x |
-2 |
-1 |
3 |
5 |
|
f1 (x) |
-3,4 |
-1,7 |
5,1 |
8,5 |
Trouver la
relation : f1 (x) =
|
x |
-2 |
-1 |
3 |
5 |
|
f 2 (x) |
1,6 |
0,8 |
- 2,4 |
-4 |
Trouver la
relation : f2 (x) =
|
2°) On donne
les expressions des fonctions g1
et g2 |
g1 (x) = 2,3 x
; complιter le tableau
|
(x) |
-1,8 |
-0,3 |
|
|
1,75 |
3 |
|
g1 (x) |
|
|
1,84 |
|
|
|
g2 (x) = - 1,5
x ; complιter le tableau
|
(x) |
-1,8 |
-0,3 |
|
|
1,75 |
3 |
|
g2 (x) |
|
|
1,84 |
|
|
|
Cliquez ici : pour faire en plus
++++
SUJET 2
|
TC2 |
E |
T |
C |
|
1°) On donne
les tableaux de variation des fonctions f1 et f2 |
|
|
|
|
|
x |
-3 |
-1 |
2 |
3,5 |
|
f1 (x) |
-3,6 |
-1,2 |
2,4 |
4,2 |
|
x |
-3 |
-1 |
2 |
3,5 |
|
f 2 (x) |
2,4 |
0,8 |
- 1,6 |
-2,8 |
|
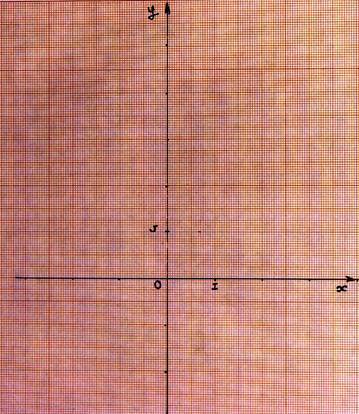
Faire la
reprιsentation graphique de chaque fonction |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
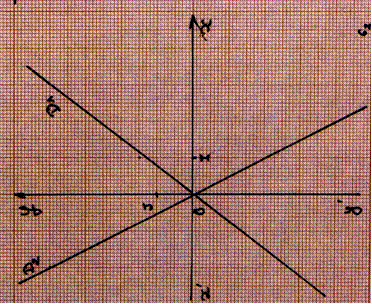
2°)
suite : Les droites
D1 et D2 reprιsentent les fonctions g1 et g2 |
Complιter le
tableau
|
(x) |
-2,2 |
|
1,5 |
|
|
|
|
g1 (x) |
|
-1 |
|
3 |
|
|
g2 (x) = - 1,5
x ; complιter le tableau
|
(x) |
-2 |
|
|
0,5 |
|
|
|
g2 (x) |
|
2 |
0 |
|
-2,6 |
|
SUJET 3
|
TC2 |
E |
T |
C |
|
1°) On donne
les ιquations des fonctions f1
et f2 |
|
|
|
|
|
A ) Faire la reprιsentation graphique de chaque
fonction |
|
|
f1
(x) = 2x et f 2 (x)
= -x |
|
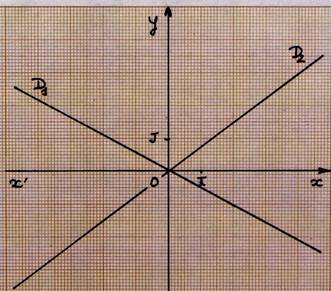
B ) Les
droites D1 et D2 reprιsentent les
fonctions g1 et g2 dιterminer les expressions : |
|
|
g1
(x) = et g 2 (x)
= |
SUJET 3 (suite )
|
TC2 |
E |
T |
C |
|
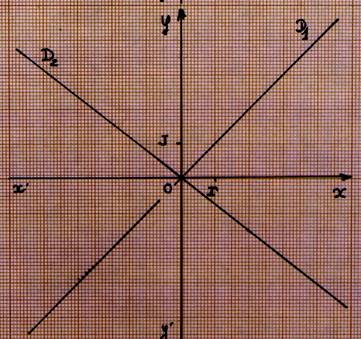
2 ° )Les droites D1 et D2 sont les reprιsentations
graphiques des fonctions g1
et g2 dιterminer
les relations : |
|
|
|
|
|
|
|
|
g1
(x) = et g 2 (x)
= |
|
|
Zone de calcul de g1
(x) = |
Zone de calcul de g 2 (x) = |
SUJET 4 (situation 6 )
|
TC2 |
E |
T |
C |
|
Nature dune
fonction : ( est-elle linιaire ou pas ?) |
|
|
|
|
Dιterminer la nature des
fonctions f1 ; f2 ;
f3 ; donnιes par les tableaux de variations suivants et
justifier :
|
x |
-2 |
2 |
4 |
6 |
|
f1
(x) |
-1,5 |
1,5 |
3 |
4,5 |
|
x |
-4 |
-3 |
2 |
9 |
|
f2 (x) |
2 |
1,5 |
-1 |
-4,5 |
|
x |
-4 |
6 |
10 |
14 |
|
f3 (x) |
-3,5 |
5,25 |
8,75 |
12,25 |
SUJET 5 (situation 6 )
|
TC2 |
E |
T |
C |
|
Nature dune
fonction : ( est-elle linιaire ou pas ?) |
|
|
|
|
Dιterminer les relations qui
lient f1 (x); f2 (x) ; f3 (x) ΰ
« x » si elles existent :
Vois cas par cas :
|
x |
-2 |
2 |
4 |
6 |
|
f1
(x) |
-1,5 |
1,5 |
3 |
4,5 |
|
x |
-4 |
-3 |
2 |
9 |
|
f2 (x) |
2 |
1,5 |
-1 |
-4,5 |
|
x |
-4 |
6 |
10 |
14 |
|
f3
(x) |
-3,5 |
5,25 |
8,75 |
12,25 |
SUJET 6 (situation 6 )
|
TC2 |
E |
T |
C |
|
1°) Reprιsenter graphiquement les fonctions
donnιes par les tableaux |
|
|
|
|
Tableau 1
|
x |
-2,5 |
-2 |
-1 |
1 |
2 |
|
f1
(x) |
-1,5 |
1,5 |
3 |
2 |
5 |
Tableau 2
|
x |
-3 |
-2 |
1 |
1,5 |
2 |
|
f2
(x) |
-2,6 |
-1,4 |
2,2 |
2,8 |
3,4 |
Tableau 3
|
x |
-3 |
-2 |
1 |
2,5 |
3,5 |
|
f3
(x) |
3,6 |
2,4 |
-1,2 |
-3 |
-4,2 |
|
2°) Quelle est la nature de ces
fonctions ? |
|
|
f1
Pourquoi ?________________________________ f2 :
. Pourquoi ? _______________________________ f3 :
Pourquoi ?________________________________ |
|