>>> CORRIGE

Sont concernées les spécialités suivantes :

l Logistique et commercialisation

l Métiers de la comptabilité

l Vente-Action marchande

Le sujet comporte 7 pages numérotées de 1/7 à 7/7. Le formulaire est en dernière page.

La clarté des raisonnements et la qualité de la rédaction interviendront pour une part importante dans l’appréciation des copies.

Les candidats répondent sur une copie à part et joignent les annexes.

L’usage de la calculatrice est autorisé.

Exercice 1 (7,5 points)

Une entreprise assurant le service restauration à bord des trains de voyageurs souhaite renforcer son offre. Elle effectue une étude statistique des distances, en km, parcourues par des voyageurs en train. L’histogramme ci-dessous présente les résultats de cette étude.

1.1. Donner la nature (qualitative ou quantitative, continue ou discontinue) du caractère statistique étudié.

1.2. Compléter les colonnes, sauf la dernière, du tableau statistique de l’annexe 1 page 5/7 à rendre avec la copie.

1.3. Calculer la distance moyenne. On admet que toutes les distances comptées dans une même classe sont égale au centre de la classe. Le candidat peut utiliser les fonctions statistiques de la calculatrice et écrire directement la valeur de.

1.4. Compléter le polygone des fréquences cumulées croissantes de l’annexe 1 page 5/7 à rendre avec la copie.

1.5. Déterminer, en utilisant le polygone des fréquences cumulées croissantes, la valeur d_M de la médiane. Laisser apparent les traits de construction utiles à la détermination. Donner une signification de cette valeur.

1.6. L’entreprise décide de renforcer son effort de service restauration sur les lignes de chemin de fer où la distance parcourue appartient à la même classe que la moyenne et la médiane. Déterminer cette classe à l’aide du tableau statistique de l’annexe 1 page 5/7

Exercice 2 (5 points)

On considère que le prix y, en €, du billet de train est proportionnel à la distance parcourue x en km. Le coefficient de proportionnalité qui permet de passer de la distance parcourue au prix est égal à 0,12.

2.1. Compléter le tableau de proportionnalité de l’annexe 2 page 6/7 à rendre avec la copie.

2.2. Placer les trois points de coordonnées (x ; y) dans le plan rapporté au repère de l’annexe 2 page 6/7 à rendre avec la copie.

2.3. Les trois points de coordonnées (x ; y) appartiennent à la représentation graphique de la fonction f définie par f (x) = 0,12x pour x compris entre 0 et 750.

2.3.1. Représenter graphiquement f pour x compris entre 0 et 750 à l’aide du repère de l’annexe 2 page 5/6.

2.3.2. Déterminer graphiquement l’abscisse du point de la représentation graphique de f qui a pour ordonnée 42. Laisser apparent les traits utiles à la détermination.

2.4. Le En déduire la plus grande distance qu’il est possible de parcourir avec 42 €.

Exercice 3 (7,5 points)

Pour les vacances, une famille composée de 2 adultes et de 2 enfants décide de partir à la découverte de certaines épaves de la côte atlantique. Le centre de plongée sous-marine propose le tarif suivant :

- Pension complète : 270 € par adulte et 160 € par enfant.

- Forfait de 10 plongées encadrée : 121 € par adulte et 82 € par enfant.

- Trajet aller-retour en TGV atlantique : 156 € pour l’ensemble de la famille.

3.1. Calculer, pour cette famille, le coût total C du séjour comprenant la pension complète, les forfaits de 10 plongées encadrées et le trajet aller-retour en TGV atlantique.

3.2. Le jour de la réservation il faut verser un acompte égal à 20 % du coût total du séjour. Calculer le montrant M de l’acompte à verser le jour de la réservation.

3.3. Pour payer les 1 137,60 € restant, la famille choisit le paiement à crédit sous la forme de 4 mensualités égales. La première est payable un mois après la réservation du séjour. La détermination du montant x des mensualités conduit à écrire :

4x - (1 + 2 + 3 + 4) x= 1 137,6

3.3.1. Montrer que cette équation peut s’écrire : 3,95x = 1 137,6

3.3.2. Résoudre cette équation et donner le montant des mensualités.

3.4. En prévision de ce séjour la famille avait placé 560 € pendant 2 ans à intérêts composés au taux annuel de 3,5 %.

3.4.1. Calculer la valeur acquise A par ce placement. Arrondir la valeur au centime.

3.4.2. Cette valeur acquise permettra-t-elle de payer l’acompte et la première mensualité. Justifier la réponse.

ANNEXE 1 (À rendre avec la copie)

Distance parcourue en km	Fréquence %	Fréquence cumulé croissant %	Effectif ni	Centre de la classe xi
[0 ; 200[	22	22	264	100
[200 ; 400[	40	62	480	300
[400 ; 600[			312
[…… ; ……[
Total	100		1 200

Polygone des fréquences cumulées croissante de l’exercice 1.

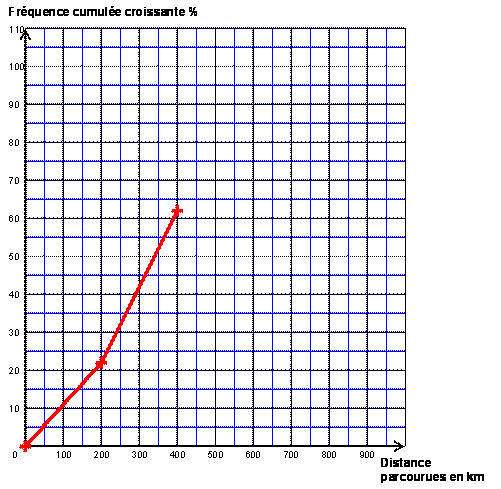
ANNEXE 2 (À rendre avec la copie)

Tableau de proportionnalité de l’exercice 2

Distance parcourue en km, x	100	200	300
Prix du billet en €, y

Repère de l’exercice 2

FORMULAIRE DE MATHÉMATIQUES

BEP DU SECTEUR TERTIAIRE

Identités remarquables

(a+b)² = a² + 2ab + b² ;

(a-b)² = a² - 2ab + b² ;

(a+b)(a-b) = a² - b².

Puissances d'un nombre :

(ab)^m = a^mb^m  ; a^m+n = a^m ´ aⁿ  ; (a^m)ⁿ = a^mn

Racines carrées :

= ; =

Suites arithmétiques :

Terme de rang 1 : u₁ et raison r

Terme de rang n :

u_n = u_n-1 + r

u_n = u₁ + (n–1)r

Suites géométriques :

Terme de rang 1 : u₁ et raison q

Terme de rang n :

u_n = u_n-1q

u_n = u₁.q^n-1

Statistiques :

Moyenne

Écart type :

Relations métriques dans le triangle rectangle :

AB² + AC² = BC²

AH . BH = AB . AC

sin = ; cos = ; tan =

Calcul d’intérêts :

C : capital ; t : taux périodique ;

n : nombre de périodes ;

A : valeur acquise après n périodes.

Intérêts simples	Intérêts composés :
I = Ctn A = C + I	A = C(1 + t)^n